Question

The slope of line m is 5.

Which lines are parallel to line l?
Select each correct answer.
line p, which contains the points (6, 4) and (11, 3)
line q, which contains the points (3, 1) and (4, 6)
line k, which contains the points (4, 15) and (2, 5)
line n, which contains the points (3, 6) and (8,7)

Answer 1

To determine which lines are parallel to line l, we need to check if their slopes are equal.

Given that the slope of line m is 5, we can compare it with the slopes of the other lines:

line p: slope = (3 - 4) / (11 - 6) = -1 / 5
line q: slope = (6 - 1) / (4 - 3) = 5 / 1 = 5
line k: slope = (5 -15) / (2 - 4) = -10 / -2 = 5
line n: slope = (7 - 6) / (8 - 3) = 1 / 5

BasedTo determineTo which determine which lines on the calculations:

lines are are parallel- Line parallel p has a to line l, slope of - we need1 to line l, to/ we need to find5 compare, lines which their with slopes is not the. equal same If to slope the two slope lines as line l.

of have the same slopeGiven that, the line l (5 they slope). are of Therefore parallel, line.

m line is pGiven is that the5 not parallel, slope of to line line m l is we need to find.
lines - Line5 with, a q has we slope need a of slope to check5 of .

Let5 the slopes of's the, which calculate other the is slope lines of.

Line each p line::

equal to the slope of line TheLine l slope p.: of slope Therefore line, p line can q = ( be3 is calculated - parallel using the to4 line formula) / l:.
slope ( =-11 Line ( - ky has26 a -) slope y = - of 11)5 / /, ( 5x2
-Line x1 q which: is equal to)
the slope of line slope =Using l the (6. Therefore points (,6 line, - 1) k is4) parallel to / (4 line and - ( l11 .
,-3 ) Line3 = n):
has slope a5 = / slope of ( 131 - = / 455),
which / is ( not equal to the11 - 6 slope) of line = - l1 ( /5 Line k: slope = (5 - 15)5). Therefore =, line / - ( n2 -0 is4. not parallel) = to line - l10.

/ -2So, the = lines2

Line q: Using the points (3 parallel to5 line
Line n: l are line slope q and = ( line k7. - 6) /, 1) and (4, 6):
slope = ( (68 - - 13)) / (4 = 1 / 5

Lines p, q, and k have a slope of 5, which is - 3) = the 5 / 1 = 5 same

Line k: Using the as the slope of line points (4, 15) and ( l.2, Therefore 5, lines p):
,slope = q, (5 and - k are15 parallel) / (2 to line l.

- So,4 the) correct = answers are: -10 / -2 line p, = 5 line q,

Line n: Using and line k. the points (3, 6) and (8, 7):
slope = (7 - 6) / (8 - 3) = 1 / 5 = 0.2

Now, comparing the slopes:

- Line p has a slope of -0.2, which is not equal to the slope of line m (5). Therefore, line p is not parallel to line l.

- Line q has a slope of 5, which is equal to the slope of line m (5). Therefore, line q is parallel to line l.

- Line k has a slope of 5, which is equal to the slope of line m (5). Therefore, line k is parallel to line l.

- Line n has a slope of 0.2, which is not equal to the slope of line m (5). Therefore, line n is not parallel to line l.

Based on the comparison of slopes, the correct answers are:

- Line q, which contains the points (3, 1) and (4, 6)
- Line k, which contains the points (4, 15) and (2, 5)

Answer 2

Answer: Lines q and k

Detailed explanation:

We're asked to find the slope of the line that's parallel to line m, given that m's slope is 5.

The important thing to realize is that parallel lines have equal slopes.

This means that if a line is parallel to line m, then it's going to have the same slope as line m.

Let's find the slope of each of these lines.

`\hrulefill`

LINE P

We're given that line p has the following points:
`\sf{(6,4)\:and\:(11,3)}`.

To find line p's slope I use the formula:

`\bf{m=(y_2-y_1)/(x_2-x_1)}`

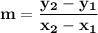
Plug in the data:

`\bf{m=(3-4)/(11-6)=(-1)/(5)=-(1)/(5)}`

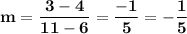
This line has a slope of -1/5, which is not equal to 5.

Therefore, line p is not parallel to line m.

`\hrulefill`

LINE Q

We're given that line q has the points
`\sf{(3,1)\:and\:(4,6)}`.

Once again, I use the slope formula:

`\bf{m=(6-1)/(4-3)=(5)/(1)=5}`

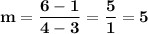
Since this line has a slope of 5, it's parallel to line m.

`\hrulefill`

LINE K

We know that line k contains the points (4,15) and (2,5).

`\bf{m=(5-15)/(2-4)=(-10)/(-2)=5}`

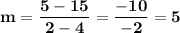
Line k is also parallel to line m.

`\hrulefill`

Finally, let's take a look at line n.

LINE N

We know that line n contains the points (3,6) and (8,7).

`\bf{m=(7-6)/(8-3)=(1)/(5)}`

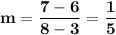
Line n is not parallel to line m.

- - - - - - - - - - - - - - -

Therefore, the lines that are parallel to line m are: lines q and k.

Have a wonderful day! :)