Question

Factor 2x^2-18x-20 and solve the factored form to turn it back into 2x^2-18x-20

Answer 1

`2(x +1)(x-10)`

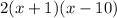
Explanation:

To factor a quadratic in the form
`ax^2 + bx + c`, we need to find two numbers that multiply to
`ac` and sum to
`b`.

For the given quadratic, 2x² - 18x - 20, the values of a, b and c are:

• a = 2
• b = -18
• c = -20

Therefore, the product of
`a` and
`c` is:

`ac=2 \cdot (-20) = -40`

So we need to find two numbers that multiply to -40 and sum to -18.

The factor pairs of -40 are:

• 40 and -1
• -40 and 1
• 20 and -2
• -20 and 2
• 10 and -4
• -10 and 4
• 8 and -5
• -8 and 5

Therefore, the two numbers that multiply to -40 and sum to -18 are:

• -20 and 2

Rewrite the middle term of the given quadratic (-18x) using the two numbers:

`2x^2-18x-20=2x^2-20x+2x-20`

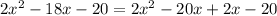
Factor the first two terms and the last two terms separately:

`=2x(x-10)+2(x-10)`

Factor out the common term (x - 10):

`=(2x+2)(x-10)`

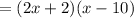
To factor further, we can factor out 2 from the first binomial:

`=2(x+1)(x-10)`

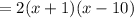
Therefore, the factored form of the given quadratic expression is:

`\large\boxed{2(x +1)(x-10)}`

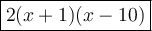
To turn it back into the original expression, use the distributive property:

`\begin{aligned}2(x+1)(x-10)&=2(x^2-10x+x-10)\\&=2(x^2-9x-10)\\&=2x^2-18x-20\end{aligned}`

Thus, the factored form 2(x + 1)(x - 10) is equivalent to the original expression 2x² - 18x - 20.