Question

2: A satellite revolving around the Earth with orbital speed 7.35 x 10³ ms-¹. Calculate its altitude. The mass and radius of Earth are 5.974 x 1024 kg and 6.378 x 106 m respectively.​

Answer 1

Approximately
`1.00* 10^(6)\; {\rm m}`.

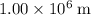Step-by-step explanation:

To find the altitude of the satellite, start by finding the radius of its orbit. Assuming that the only force on the satellite is gravitational attraction from the Earth, the orbital radius can be found from the fact that the satellite is in a centripetal motion.

Let
`r` denote the radius of the orbit. Note that
`r\!` would represent the distance between the satellite and the center of the Earth, not the altitude of the satellite relative to the surface of the Earth. To find the altitude of the satellite, subtract the radius of the Earth from the radius of this orbit.

Since the satellite is in a centripetal motion of orbital velocity
`v`, magnitude of the net force on the satellite would be:

`\displaystyle (\text{net force}) = (m\, v^(2))/(r)`,

Where:

• 
  `m` is the mass of the satellite (not given),
• 
  `v = 7.35* 10^(3)\; {\rm m\cdot s^(-1)}` is the (tangential) orbital velocity of the satellite, and
• 
  `r` is the radius of the orbit.

Under the assumptions, gravitational attraction from the Earth would be the only force on this satellite. Thus, magnitude of the net force on the satellite would also be equal to that of gravitational attraction:

`\begin{aligned}& (\text{net force}) \\ &= (\text{gravitational attraction}) \\ &= (G\, M\, m)/(r^(2))\end{aligned}`,

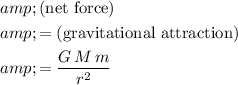Where:

• 
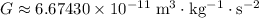  `G \approx 6.67430* 10^(-11)\; {\rm m^(3)\cdot kg^(-1)\cdot s^(-2)}` is the gravitational constant,
• 
  `M = 5.974* 10^(24)\; {\rm kg}` is the mass of the Earth,
• 
  `m` is the mass of the satellite (not given), and
• 
  `r` is the radius of the orbit.

Equate the two expression for the net force on the satellite and solve for the orbital radius
`r`:

`\displaystyle (G\, M\, m)/(r^(2)) = (\text{net force}) = (m\, v^(2))/(r)`.

`\begin{aligned} r &= (G\, M\, m)/(m\, v^(2)) \\ &= (G\, M)/(v^(2)) \\ &= ((6.67430* 10^(-11))\, (5.974 * 10^(24)))/((7.35* 10^(3))^(2))\; {\rm m} \\ &\approx 7.3807 * 10^(6)\; {\rm m}\end{aligned}`.

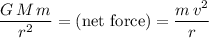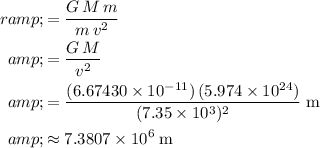Note that the mass of the satellite
`m` is eliminated and does not appear in the expression for orbital radius. In other words, the radius of the orbit at this given orbital velocity does not depend on the mass of the satellite.

The altitude of the satellite is the distance between the satellite and the surface of the Earth. The previous calculation shows that the satellite is at a distance of approximately
`7.3807 * 10^(6)\; {\rm m}` from the center of the orbit- not from the surface of the Earth.

To find altitude, subtract the radius of the Earth (distance between center of Earth and surface) from the radius of the orbit (distance between center of Earth and satellite.)

`\begin{aligned} & (\text{altitude}) \\ =\; & (\text{orbital radius}) - (\text{radius of planet}) \\ \approx \; & (7.3807* 10^(6)\; {\rm m}) - (6.378* 10^(6)\; {\rm m}) \\ \approx\; & 1.00 * 10^(6)\; {\rm m}\end{aligned}`.

Hence, the altitude of the satellite would be approximately
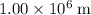`1.00 * 10^(6)\; {\rm m}`.