Question

Functions f(x) = 3x + 11 /X-3 and g(x)= X-2/ 2 .If f(4) = g(x + 1), find the value of x.
​

Answer 1

To find the value of x, we substitute the given values into the equations.

Explain:
f(x) = (3x + 11)/(x - 3)
g(x) = (x - 2)/2
f(4) = g(x + 1)

Substitute x = 4 into f(x):
f(4) = (3(4) + 11)/(4 - 3) = (12 + 11)/(1) = 23/1 = 23

Next, substitute the value we calculated for f(4) into g(x + 1):
23 = (x + 1 - 2)/2 = (x - 1)/2

Now, we can solve for x:
Multiply both sides of the equation by 2:
2 * 23 = x - 1
46 = x - 1

Add 1 to both sides of the equation:
46 + 1 = x
47 = x

Therefore, the value of x is 47.

Hope this help

Answer 2

x = 47

`\hrulefill`

Explanation:

Given functions:

`f(x)=(3x+11)/(x-3)`
`g(x)=(x-2)/(2)`

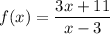
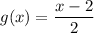
Calculate the value of f(4) by substituting x = 4 into function f(x):

`\begin{aligned}f(4)&=(3(4)+11)/(4-3)\\\\&=(12+11)/(1)\\\\&=(23)/(1)\\\\&=23\end{aligned}`

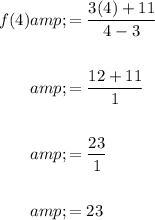
Find the expression for g(x + 1) by substituting x = x + 1 into function g(x):

`\begin{aligned}g(x+1)&=((x+1)-2)/(2)\\\\&=(x+1-2)/(2)\\\\&=(x-1)/(2)\end{aligned}`

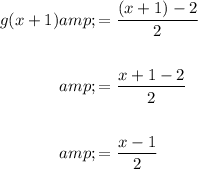
To find the value of x when f(4) = g(x + 1), substitute the found value of f(4) and the found expression for g(x + 1) into the equation, and solve for x:

`\begin{aligned}f(4)&=g(x+1)\\\\23&=(x-1)/(2)\\\\23 \cdot 2&=(x-1)/(2)\cdot 2\\\\46&=x-1\\\\46+1&=x-1+1\\\\47&=x\\\\x&=47\end{aligned}`

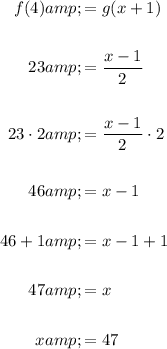
Therefore, the value of x is 47.