Heya There!
Question:
The sides of a triangular field are 41m,40m and 9m.find the number of rose beds that can be prepared in the field, if each rose bed, on an average needs 900cm^2 space.
Answer:
No of rose beds = 2000
Step-by-step Explanation:
If a,b,c are the sides of a triangle and s is the semi-perimeter, then it's area ∆ is given by using Heron's Formula,
∆ = √s (s-a) (s-b) (s-b)
where,
s = semi-perimeter
a = length of side a
b = length of side b
c = length of side c
Here given,
a = 41, b = 40 and c = 9
→ s = ½ ( a + b + c )
→ s = ½ ( 41 + 40 + 9 ) = 45
Now, By using Heron's Formula,
∆ = √s (s-a) (s-b) (s-b)
∆ = √ 45 ( 45 - 41 ) ( 45 - 40 ) ( 45 - 9 )
∆ = √ 45 x 4 x 5 x 36
∆ = √ 3² x 5 x 2² x 5 x 2² x 3²
∆ = 3² x 2² x 5
∆ = 180 m²
Now,
Area of each rose bed = 900cm²
converting 900cm² to m²:

Number of rose beds:
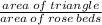
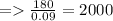
Hence, the number of rose beds is 2000..
More information about Heron's Formula:
- Heron's formula is a formula for calculating the area of a triangle in terms of the lengths of its sides ..
- In symbols, if a, b, and c are the lengths of the sides:- Area = Square root of√s(s - a)(s - b)(s - c), where s is half the perimeter, or (a + b + c)/2 or ½(a+b+c) ..
- Heron's Formula was discovered by Heron of Alexandria (also known as Hero of Alexandria) who was a Greek Engineer and Mathematician.
- He found the area of the triangle using only the lengths of its sides which made it possible to apply to any type of triangle be it, equilateral, isosceles, or scalene...
Hope this helps you :)