Question

10. PLS HELP [10 points]

A straight line passes through points (1, 15) and (5, 3). What is the equation of the line?
Oy=2x+18
Oy=-3x+18
O y = 3x+18
y = -7x+18

Answer 1

Given to us that:—

• A straight line passes through (1,15) and (5,3)

To find:—

• The equation of the line

Gradient (m) of the line:

⇆
`m=\cfrac{y_2-y_1}{x_2-x_1}`

⇆
`m=\cfrac{3-15}{5-1}=\cfrac{-12}{4}=-3}`

So , The gradient is -3 . Now , Let's write the equation of this line in the form of pointslope:—

⇆
`y-y_1=m(x-x_1)`

⇆
`y - 3 = -3(x - 5)`

⇆
`y - 3 = -3x + 15`

⇆
`y = -3x + 15 + 3`

⇆
`y = -3x + 18`

Henceforth , Equation : y = -3x + 18 .

Answer 2

y = -3x + 18

Explanation:

Pre-Solving

We are given that a line passes through (1, 15) and (5, 3).

We want to write the equation of the line.

There are multiple ways to write the equation of the line, but let's write it in slope-intercept form, which y=mx+b where m is the slope and b is the value of y at the y-intercept.

Solving

Slope

Let's first find the slope of the line.

The slope can be found using the following equation:

`m=(y_2-y_1)/(x_2-x_1)`

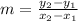
Let's label the values of the points, then plug into the equation.

`x_1=1\\y_1=15\\x_2=5\\y_2=3`

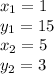
Now, substitute.

`m=(3-15)/(5-1)`

`m=(-12)/(4)`

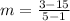
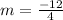
Divide.

m = -3

Now, substitute into the equation.

We get:

y = -3x + b

We now need to find b.

Y-intercept

As the line passes through both (1, 15) and (5, 3), we can use either point to get the value of b.

Taking (5,3) for example:

3 = -3(5) + b

Multiply.

3 = -15 + b

Add 15 to both sides.

18 = b

Substitute 18 as b.

y = -3x + 18