Question

The function f is defined by f(x) = 2x³ + 3x² + cx + 8, where c is a constant. In the xy-plane, the graph of f intersects the x-axis at the three points (−4, 0), (1/2, 0), and (p, 0). What is the value of c?​

no answer from internet please

Answer 1

• A. -18

Step-by-step explanation:

Given the function
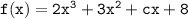`\tt{f(x) = 2x^3 + 3x^2 + cx + 8}` and the x-intercepts
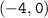`\tt{(-4, 0)}` and
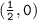`\tt{((1)/(2), 0)}`, we can find the value of c.

To find the value of c, we can use the fact that the product of the roots of a cubic equation is equal to the constant term divided by the coefficient of the highest power of
`\bf{x}`.

In this case:

• the constant term = 8
• the coefficient of the highest power of x = 2

Using the given x-intercepts, we have:

1.
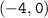`\tt{(-4, 0)}`: This means that when
`\tt{x = -4}`, the function
`\tt{f(x)}` equals 0.

Plugging this into the equation, we get:

• 
  `\tt{f(-4) = 2(-4)^3 + 3(-4)^2 + c(-4) + 8 = 0}`

Simplifying this equation, we get:

• 
  `\tt{-128 + 48 - 4c + 8 = 0}`

• 
  `\tt{-72 - 4c = 0}`

• 
  `\tt{-4c = 72}`

• 
  `\tt{c = -18}`

Therefore, the value of c is -18.

________________________________________________________

Full Question