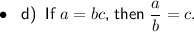Question

!50 POINTS! (3 SIMPLE GEOMETRY QUESTIONS)

(I MARKED THE RED X ON THE ANSWER CHOICES I KNOW ARE WRONG TO HELP YOU)

QUESTIONS BELOW
|
|
\/

Answer 1

`\textsf{14)}\;\;(4000)/(81)\pi \; \textsf{cm}^3 \approx 49.4\pi\; \sf cm^3`

`\textsf{1)\;\;c)\;\;If the measure of an angle is not $90^(\circ)$, then it is not a right angle.}`

`\textsf{3)\;\;d)\;\;If\;$a=bc$,\;then\;$(a)/(b)=c$.}`

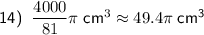
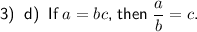
Explanation:

Question 14

The formula for the lateral area of a cone is:

`\large\boxed{L.A.=\pi r l}`

where:

• r is the radius of the circular base.
• l is the slant height.

If a cone has a slant height of 18 cm and a lateral area of 60π cm², then we can find its radius (r) by substituting the given values into the formula and solving for r:

`\begin{aligned}\pi r \cdot 18&=60 \pi\\\\18r&=60\\\\(18r)/(18)&=(60)/(18)\\\\r&=(10)/(3)\; \sf cm\end{aligned}`

Therefore, the radius of the circular base of the cone is 10/3 cm.

The formula for the volume of a sphere is:

`\large\boxed{V=(4)/(3)\pi r^3}`

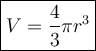
where r is the radius.

To calculate the volume of a sphere with a radius equal to that of the cone, substitute the found radius of the cone (r = 10/3) into the volume of the sphere formula:

`\begin{aligned}V&=(4)/(3)\pi \cdot \left((10)/(3)\right)^3\\\\&=(4)/(3)\pi \cdot \left((100)/(27)\right)\\\\&=(4000)/(81)\pi\\\\&\approx 49.4\pi\; \sf cm^3\;(nearest\;tenth)\end{aligned}`

Therefore, the volume of the sphere is exactly (4000/81)π cm³, or approximately 49.4π cm³.

`\hrulefill`

Question 1

The inverse of a statement is formed by negating both the hypothesis (the "if" part) and the conclusion (the "then" part) of the original statement.

The original statement is:

• If the measure of an angle is 90°, then it is a right angle.

Therefore, the hypothesis is "the measure of an angle is 90°," and the conclusion is "it is a right angle."

Negate both parts of the original statement to find the inverse:

• The negation of the hypothesis is "the measure of an angle is not 90°."
• The negation of the conclusion is "it is not a right angle."

Therefore, the inverse of the statement is:

• c) If the measure of an angle is not 90°, then it is not a right angle.

`\hrulefill`

Question 3

The converse of a statement is formed by interchanging the hypothesis (the "if" part) and the conclusion (the "then" part) of the original statement.

The original statement is:

`\bullet \;\;\;\textsf{If\;$(a)/(b)=c$,\;then\;$a=bc$.}`

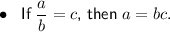
To find the converse of this statement, simply interchange the hypothesis and the conclusion. Therefore, the converse of the statement is:

`\bullet \;\;\;\textsf{d)\;\;If\;$a=bc$,\;then\;$(a)/(b)=c$.}`