Question

!50 POINTS! (3 SIMPLE GEOMETRY QUESTIONS)

QUESTIONS BELOW
|
|
\/

Answer 1

1st question: c. 6 ft by 8 ft by 10 ft

2nd Question: d. 6 inches.

3rd Question: c. 8.5 cm, 17 cm, 10.6 cm

Explanation:

For 1st Question:

To determine if a set of three side lengths can form a triangle, we need to apply the triangle inequality theorem, which states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.

Let's check each option:

a. 8 ft by 12 ft by 20 ft

`\sf 8 + 12 > 20 (False)\\ \sf 8 + 20 > 12 (True)\\ \sf 12 + 20 > 8 (True)`

These dimensions cannot form a triangle.

b. 4 ft by 5 ft by 10 ft:

`\sf 4 + 5 > 10 (False)\\ \sf 4 + 10 > 5 (True)\\\sf 5 + 10 > 4 (True)`

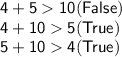
These dimensions cannot form a triangle.

c. 6 ft by 8 ft by 10 ft:

`\sf 6 + 8 > 10 (True)\\ \sf 6 + 10 > 8 (True)\\\sf 8 + 10 > 6 (True)`

These dimensions can form a triangle.

d. 6 ft by 6 ft by 12 ft:

`\sf 6 + 6 > 12 (False)\\\sf 6 + 12 > 6 (False)\\\sf 6 + 6 > 12 (False)`

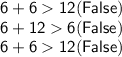
These dimensions cannot form a triangle.

So, the possible dimensions for John's triangular garden is:

c. 6 ft by 8 ft by 10 ft

`\hrulefill`

For 2nd Question:

To find the side that cannot be the length of the remaining side of the triangle, we need to apply the triangle inequality theorem, which states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.

Let the two given sides be 14 inches and 8 inches.

Now, we need to check each option:

a. 21 inches:

`\sf 14 + 8 > 21 (True)\\\sf 14 + 21 > 8 (True)\\\sf8 + 21 > 14 (True)`

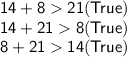
The side length 21 inches can be the length of the remaining side.

b. 14 inches:

`\sf 8 + 14 > 14 (True)\\\sf 14 + 14 > 8 (True)\\\sf 8 + 14 > 14 (True)`

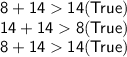
The side length 14 inches can be the length of the remaining side.

c. 8 inches:

`\sf 8 + 14 > 8 (True)\\\sf 14 + 8 > 8 (True)\\\sf 8 + 8 > 14(True)`

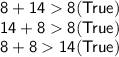
The side length 8 inches can be the length of the remaining side.

d. 6 inches:

`\sf 8 + 6 > 14 (False)\\\sf 6 + 14 > 8 (True)\\ \sf 8 + 14 > 6(True)`

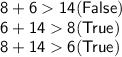
The side length 6 inches cannot be the length of the remaining side.

So, the length that cannot be the length of the remaining side of the triangle is:

d. 6 inches.

`\hrulefill`

For 3rd Question:

To determine if a set of three side lengths can form a triangle, we need to apply the triangle inequality theorem, which states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.

Let's check each option:

a. 9 cm, 11 cm, 21 cm:

`\sf 9 + 11 > 21 (False)\\ \sf 9 + 21 > 11 (True)\\\sf 11 + 21 > 9 (True)`

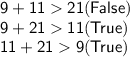
These lengths cannot form a triangle.

b. 6 cm, 14 cm, 8 cm:

`\sf 6 + 14 > 8 (True)\\\sf 6 + 8 > 14 (False)\\\sf 14 + 8 > 6 (True)`

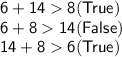
These lengths cannot form a triangle.

c. 8.5 cm, 17 cm, 10.6 cm:

`\sf8.5 + 17 > 10.6 (True)\\\sf 8.5 + 10.6 > 17 (True)\\ \sf 17 + 10.6 > 8.5 (True)\\`

These lengths can form a triangle.

d. 14 cm, 4.7 cm, 4.7 cm:

`\sf 14 + 4.7 > 4.7 (True)\\\sf 14 + 4.7 > 4.7 (True)\\\sf 4.7 + 4.7 > 14 (False)`

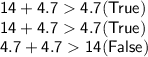
These lengths cannot form a triangle.

So, options could be the lengths of three sides of a triangle:

c. 8.5 cm, 17 cm, 10.6 cm