Question

!50 POINTS! (3 SIMPLE GEOMETRY QUESTIONS)

QUESTIONS BELOW
|
|
\/

Answer 1

1. 125

This is because as the radius grows, so does the volume, and it does so exponentially.

The volume of the smaller sphere with a radius of 2 was 33.51, and the volume of the much bigger sphere with a radius of 10 was 4188.51

By diving 4188 and 33, you get around 125.

________________________________________________________

2. 512

Lets find the volume of the original cube: 16*16*16 = 4096

The other cube has its dimentions cut in half, so now all its sides are only 8 inches.

8*8*8 = 512

________________________________________________________

3. 923.6

We know that the height is 14 and the radius is 7, so we can just use the SA of a cylinder formula to get our answer.

_____________________________________________________

~~~Harsha~~~

Answer 2

1st question: c. 125
2nd question: d. 512

3rd question:
`\boxed{\sf 293.6 in^2}`

Explanation:

For 1st Question:

The volume of a sphere is given by the formula:

`\boxed{\sf Volume = (4)/(3) * \pi * radius^3}`

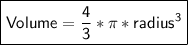
Let's calculate the volumes of Sphere A and Sphere B and then find the ratio of their volumes.

For Sphere A:

Radius of Sphere A = 2 inches

`\sf \textsf{Volume of Sphere A} = (4)/(3) * \pi * 2^3= (32)/(3) \pi \:in^3`

For Sphere B:

Radius of Sphere B = 10 inches

`\textsf{Volume of Sphere B = }\sf(4)/(3) * \pi * 10^3= (4000)/(3) \pi \:in^3`

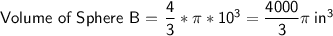
Now, to find how many times larger the volume of Sphere B is divided by Sphere A,

`\textsf{Times larger }=\frac{\textsf{ Volume of Sphere B }}{\textsf{ Volume of Sphere A}}`

`\sf \textsf{Times Larger} = ((4000)/(3))/((32)/(3))=(4000)/(3)*(3)/(32)=125`

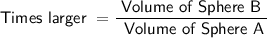
Therefore, The volume of Sphere B is 125 compared to the volume of Sphere A.

So, Answer is c. 125

`\hrulefill`

For 2nd question:

When you divide each side length of a cube by 2, you are essentially reducing the size of each dimension by half.

The new cube will have side lengths equal to half of the original cube.

Original cube side length = 16 inches

`\sf \textsf{New cube side length} = (16)/(2)\: inches =8\: inches`

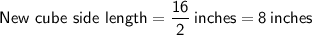
The volume of a cube is given by the formula:

Volume = side length^3

For the new cube:

`\sf Volume = 8^3`

Volume = 512 cubic inches

Therefore, the volume of the new cube with side length 8 inches will be 512 cubic inches.

So, answer is d. 512

`\hrulefill`

For 3rd question:

Given:

Radius(r) = 7 in

height(h) = diameter = 2*r =2*7=14 in

Total surface area of cylinder = ?

we have:

`\boxed{\textsf{Total Surface Area} \sf = 2\pi r(h + r)}`

where:

• r = radius of the cylinder
• h = height of the cylinder

The total surface area of a cylinder is the sum of the lateral surface area and the two end surface areas. The lateral surface area is the same as the area of a rectangle with height equal to the height of the cylinder and width equal to the circumference of the base.

Now

Substituting value

`\sf \textsf{Total Surface Area }= 2 * \pi* 7 * (14+ 7) = 293.6 in^2`

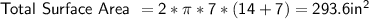
Therefore, Total surface area of cylinder is 293.6 in^2