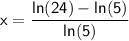Question

Use logarithms to solve for X: 5^x+1=24

Answer 1

x =
`(log24-log5)/(log5)`

Explanation:

using the rules of logarithms

• log (xy) = log x + log y

• log
`x^(n)` = n log x

note that
`5^(x+1)` =
`5^(x)` ×
`5^(1)` ( rule of exponents )

given

`5^(x+1)` = 24 ( take log of both sides )

log (
`5^(x+1)` ) = log24

log (
`5^(x)` • 5 ) = 24 ← using the above rule of logarithms , then

log
`5^(x)` + log5 = log24

x log5 + log5 = log 24 ( subtract log5 from both sides )

x log5 = log24 - log5 ( divide both sides by log5 )

x =
`(log24-log5)/(log5)`

Answer 2

`\sf x =(ln(24)-ln(5))/(ln(5))`

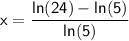
Explanation:

The equation
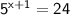`\sf 5^(x+1)=24` can be written in logarithmic form as follows:

`\sf log_5(24) = x+1`

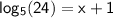
To solve for x, we can take the logarithm of both sides of the equation.

The natural logarithm (ln) is a common base for logarithms, so we can use ln(24) to represent
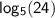`\sf log_5(24)`. This gives us the following equation:

`\sf ln(24) = ln(5^(x+1))`

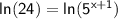
We can use the following property of logarithms to simplify the right-hand side of the equation:

`\boxed{\sf ln(a^b) = b*ln(a)}`

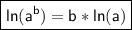
In this case, a=5 and b=x+1, so we have:

`\sf ln(24) = (x+1)*ln(5)`

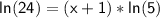
Isolating x on the left-hand side, we get:

`\sf x =(ln(24))/(ln(5)) - 1`

`\sf x =(ln(24)-ln(5))/(ln(5))`

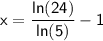
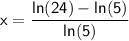
Plugging this into a calculator, we get x≈0.9746358687

Therefore, the solution to the equation 5^(x+1)=24 in logarithmic form is:

`\sf x =(ln(24)-ln(5))/(ln(5))`