Question

Can you also show work when solving it please.

Answer 1

Problem 1:

A = 55°; B = 43°; C = 82°

a = BC = 8; b = AC = 6.7; c = AB = 9.7

Explanation:

Let a = BC; b = AC; c = AB.

Let A = m<A; B = m<B; C = m<C.

The Law of Sines:

`(\sin A)/(a) = (\sin B)/(b) = (\sin C)/(c)`

In order to use the Law of Sines, you must have the measure of one angle and the length of its opposite side to establish the ratio. Then, depending on which other side or angle you are given, you can use the Law of Sines to find what is asked in the problem.

Problem 1.

Given:

A = 55°, a = 8; this establishes a ratio.

C = 82°; with this info, you can solve for c.

`(\sin A)/(a) = (\sin C)/(c)`

`(\sin 55^\circ)/(8) = (\sin 82^\circ)/(c)`

`c * \sin 55^\circ = 8 * \sin 82^\circ`

`c = (8 \sin 82^\circ)/(\sin 55^\circ)`

`c = 9.7`

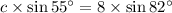
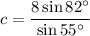
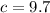
Since we have the measures of two angles (A and C), we can find the measure of the third angle (B). Then we use the Law of Sines again to find b.

A + B + C = 180°

B = 180° - A - C

B = 180° - 55° - 82°

B = 43°

`(\sin A)/(a) = (\sin B)/(b)`

`(\sin 55^\circ)/(8) = (\sin 43^\circ)/(b)`

`b * \sin 55^\circ = 8 * \sin 43^\circ`

`b = (8 \sin 43^\circ)/(\sin 55^\circ)`

`b = 6.7`

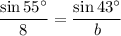
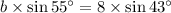
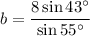
Solution:

A = 55°; B = 43°; C = 82°

a = BC = 8; b = AC = 6.7; c = AB = 9.7

Hint:

When you are solving triangles, using the Law of Sines is easier than using the Law of Cosines because the Law of Cosines is more complicated. That means that if you can use the Law of Sines, you should use it.

How can you tell if you can use the Law of Sines? It's what I stated above. If you have one side and its opposite angle, then use the Law of Sines. If you do not have a side and its opposite angle, and you have 2 sides and the included angle, then you must use the Law of Cosines.