Question

The speed of a car when passing point P is 30 ms-1 and change uniformly over a distance of

323 m to 60 ms-1. Calculate the speed of the car 3 s after passing p ?

Answer 1

Approximately
`42.5\; {\rm m\cdot s^(-1)}`.

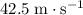Step-by-step explanation:

To find the velocity of the vehicle at the given time, start by finding the acceleration using the SUVAT equations. Since acceleration is the rate of change in velocity, the velocity after a given duration can be found by adding duration times acceleration to the initial velocity.

To find the acceleration
`a` of this vehicle, note that while initial velocity
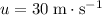`u = 30\; {\rm m\cdot s^(-1)}`, final velocity
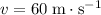`v = 60\; {\rm m\cdot s^(-1)}`, and displacement
`x = 323\; {\rm m}` are given, the time
`t` required to reach
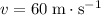`v = 60\; {\rm m\cdot s^(-1)}\!` is not given. Hence, the most suitable SUVAT equation for this setup would be the one that involves only
`a`,
`x`,
`u`, and
`v`:

`\displaystyle v^(2) - u^(2) = 2\, a\, x`.

Rearrange this equation to find acceleration:

`\begin{aligned}a &= (v^(2) - u^(2))/(2\, x) \\ &= ((60)^(2) - (30)^(2))/(323)\; {\rm m\cdot s^(-2)} \\ &\approx 4.1796\; {\rm m\cdot s^(-2)}\end{aligned}`.

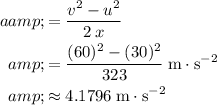In other words, the velocity of the vehicle would increase by approximately
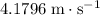`4.1796\; {\rm m\cdot s^(-1)}` every second.

If the vehicle accelerates at this rate for a duration of
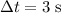`\Delta t = 3\; {\rm s}`, the velocity of the vehicle would have increased by
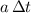`a\, \Delta t` from the initial value. Add this quantity to the initial velocity of
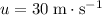`u = 30\; {\rm m\cdot s^(-1)}` to find the resultant velocity after the given duration:

`\begin{aligned} u + a\, \Delta t &\approx 30\; {\rm m\cdot s^(-1)} + (3\; {\rm s})\, (4.1796\; {\rm m\cdot s^(-2)}) \\ &\approx 42.5\; {\rm m\cdot s^(-1)}\end{aligned}`.

Thus, the velocity of the vehicle would be approximately
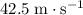`42.5\; {\rm m\cdot s^(-1)}` at the specified moment.