Answer:
see explanation
Explanation:
if the points lie on a straight line then the slopes m between consecutive points will be equal, that is
 =
=
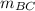
calculate slopes using the slope formula
m =
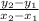
with (x₁, y₁ ) = A (a, b+c ) and (x₂, y₂ ) = B (b, c+a )
 =
=
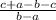 =
=
 ← factor out - 1 from each term on the denominator
← factor out - 1 from each term on the denominator
 =
=
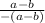 ← cancel out (a - b) on numerator/ denominator
← cancel out (a - b) on numerator/ denominator
 =
=
 = - 1
= - 1
similarly
with (x₁, y₁ ) = B (b, c + a ) and (x₂, y₂ ) = C (c, a + b )
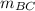 =
=
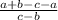 =
=
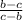 ← factor out - 1 from each term on the denominator
← factor out - 1 from each term on the denominator
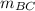 =
=
 ← cancel out (b - c ) on numerator/ denominator
← cancel out (b - c ) on numerator/ denominator
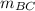 =
=
 = - 1
= - 1
since
 =
=
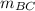 = - 1
= - 1
then the points are collinear , lie on straight line