Question

Type the correct answer in the box. Use numerals instead of words. If necessary, use / for the fraction bar.

In the given diagram, two sets of arcs are drawn above and below segment AB using a compass set to the same width. For one set of arcs, the compass needle is positioned at point A. For the second set of arcs, the compass needle is positioned at point B. A line drawn through the intersections of these two sets of arcs determines the location of point C.

A straight line A B is bisected by a perpendicular line at C. The perpendicular line is formed by connecting the intersection of two arcs above and below the line. A C is labeled as 16 units.

Answer 1

`CB = 16\\`

`AB = 32`

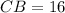
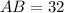
Explanation:

The line drawn on
`AB` while also passing through Point
`C` would be the perpendicular bisector of the line
`AB.`

We can create a equation with this information.

⇒ FORMULATE

`AC = CB = (1)/(2) AB`

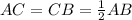
Within the given diagram, we can observe two pieces of information.

⇒
`AC = 16`

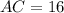
This means that ⇒
`CB = 16` .

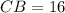Moving onto the next steps:

⇒
`AB = 2AC`

⇒
`2 * 16`

⇒
`32`

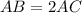
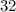
We can use the Pythagorean theorem to verify that the given measurements are consistent with the diagram.

Since AC is labeled as 16 units and CB is labeled as 16 units, we can conclude that triangle ABC is an isosceles triangle with AC = CB. Also, since the line segment AB bisects the perpendicular line at C, we know that AC and CB are equal in length and that ACB is a right angle.

Using the Pythagorean theorem, we can find the length of AB:

⇒
`AB^2 = AC^2 + CB^2`

⇒
`AB^2 = 16^2 + 16^2`

⇒
`AB^2 = 512`

⇒
`AB = 32`

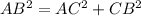
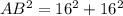
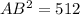
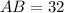
Therefore, the given measurements of CB = 16 units and AB = 32 units are consistent with the diagram.