Question

Find the area of the triangle
19cm
15cm
12cm

Answer 1

Explanation:

Answer 2

The area of the triangle with side lengths 19 cm, 15 cm, and 12 cm is approximately
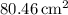`\(80.46 \, \text{cm}^2\)`, calculated using Heron's formula.

Explanation:

To find the area of a triangle given its side lengths using Heron's formula, you can use the following steps:

1. Calculate the semi-perimeter (s) of the triangle using the formula:

`\[ s = (a + b + c)/(2) \]`

where (a), (b), and (c) are the side lengths of the triangle.

2. Use Heron's formula to find the area (\(A\)):

`\[ A = √(s \cdot (s - a) \cdot (s - b) \cdot (s - c)) \]`

Given the side lengths of the triangle as 19 cm, 15 cm, and 12 cm, let's calculate:

`\[ s = (19 + 15 + 12)/(2) = 23 \, \text{cm} \]`

Now, plug the values into Heron's formula:

`\[ A = √(23 \cdot (23 - 19) \cdot (23 - 15) \cdot (23 - 12)) \]`

`\[ A = √(23 \cdot 4 \cdot 8 \cdot 11) \]`

`\[ A = √(6472) \]`

`\[ A \approx 80.46 \, \text{cm}^2 \]`

So, the area of the triangle is approximately
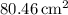`\(80.46 \, \text{cm}^2\)`.