Question

100 POINTS

For the following question, upload a scan/picture of your handwritten solution. Clearly BOX your final answer to make it obvious. Oxygen gas generated in the thermal decomposition of potassium chlorate is collected over water. At 24°C and an atmospheric pressure of 762 mm Hg, the volume of gas collected is 0.128 L. The vapour pressure of H20 at 24°C is 22.4 torr. What is the mass of oxygen collected?​

Answer 1

0.163g

Step-by-step explanation:

Given that

• total pressure: 762mmHg=1 atm (approx)
• Pressure of water vapour: 22.4 torr = 0.029 atm
• Therefore H2O pressure : 1-0.029=.971 atm
• T=24 dgree = 297K
• V=128L

Recall ideal gas law

`PV=nRT`

`\implies n=(PV)/(RT)\\\\ \therefore n=(0.971 * 0.128)/(0.0821 * 297)= \boxed{5.097* 10^(-3) }`

Remember that

• W=nM
• W=5.097*10^-3*32=0.163g

Answer 2

0.163 grams (3 s.f.)

Step-by-step explanation:

To find the mass of oxygen collected, we first need to determine the partial pressure of oxygen in the collected gas. To do this, subtract the vapor pressure of water from the total atmospheric pressure to get the pressure exerted by the oxygen gas alone.

As 1 mm Hg = 1 Torr, then 762 mm Hg = 762 Torr.

Therefore:

`\begin{aligned}\textsf{Partial pressure of oxygen}&=\sf Total\;atmospheric \;pressure - Vapor\; pressure \;of \;H_2O\\\\&=\sf 762\; Torr - 22.4\; Torr\\\\&=\sf 739.6 \;Torr\end{aligned}`

To find the number of moles of oxygen gas, use the ideal gas law.

Ideal Gas Law

`\large\boxed{PV=nRT}`

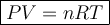
where:

• P is the pressure measured in torr (Torr).
• V is the volume measured in liters (L).
• T is the temperature measured in kelvin (K)
• R is the ideal gas constant (62.363598221529 L⋅Torr⋅K⁻¹⋅mol⁻¹)
• n is the number of moles.

Rearrange the equation to solve for n:

`n = (PV)/(RT)`

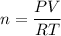
As we have been given the temperature in °C, we must first convert it to Kelvin by adding 273.15 to the Celsius value:

`\sf T= 24 + 273.15 = 297.15\;K`

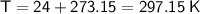
Therefore, the values to substitute into the formula are:

• P = 739.6 Torr
• V = 0.128 L
• T = 297.15 K
• R = 62.363598221529 L⋅Torr⋅K⁻¹⋅mol⁻¹

Substitute the values into the formula and solve for n:

`n = \sf (739.6 \;Torr \cdot 0.128\; L)/(62.363598221529\; L\cdot Torr\cdot K^(-1)\cdot mol^(-1)\cdot 297.15\; K)`

`n = \sf (739.6\cdot 0.128\;mol)/(62.363598221529\cdot 297.15)`

`n = \sf 0.005108577\;mol`

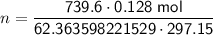
The molar mass of oxygen gas (O₂) is approximately 31.999 g/mol.

Therefore, to find the mass of oxygen collected, multiply the found number of moles (n) by the molar mass:

`\begin{aligned}\textsf{Mass of oxygen}&=\sf 0.005108577\;mol \cdot 31.999\;g \cdot mol^(-1)\\\\&=\sf 0.1634693663\;g\end{aligned}`

Therefore, the mass of oxygen collected is approximately 0.163 grams (3 s.f.).