Question

Can someone help me with this?

Answer 1

(a) v(t) = <2t, -2/t³>

(b) a(t) = <2, 6/t⁴>

(c) ||v(t)|| = √(4t² + 4/t⁶)

(d) Refer to the attached photo for the sketch.

Explanation:

To find the velocity, acceleration, and speed of a particle with the given position function, we'll need to apply some basic principles of calculus and vector operations. Let's break it down step by step:

(a) Velocity (v(t)):

Velocity represents the rate of change of position with respect to time and is defined as the derivative of the position vector r(t) with respect to time, t.

`v(t)=(dr(t))/(dt)`

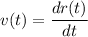
Given the position function r(t) = <t², 1/t²>, we can find the velocity vector by taking the derivative of each component with respect to time:

`\Longrightarrow v(t) = \Big < (d)/(dt)[t^2], (d)/(dt)[(1)/(t^2) ] \Big > \\\\\\\\\therefore \boxed{v(t) = \Big < 2t, -(2)/(t^3) \Big > }`

(b) Acceleration (a(t)):

Acceleration represents the rate of change of velocity with respect to time and is defined as the derivative of the velocity vector v(t) with respect to time, t.

`a(t) = (dv(t))/(dt)`

Taking the derivative of each component of the velocity vector v(t) = <2t, -2/t³> with respect to time gives us the acceleration vector:

`\Longrightarrow a(t) = \Big < (d)/(dt) [2t], (d)/(dt) [-(2)/(t^3)] \Big > \\\\\\\\\therefore \boxed{a(t) = \Big < 2, (6)/(t^4) \Big > }`

(c) Speed (||v(t)||):

Speed is the magnitude of velocity, which measures the rate at which the particle is moving without considering its direction.

The magnitude of the velocity vector v(t) is given by:

`\big|\big|v(t)\big|\big|=√((v_x)^2+(v_y)^2) \\\\\\\\\Longrightarrow \big|\big|v(t)\big|\big|=\sqrt{(2t)^2+(-(2)/(t^3) )^2} \\\\\\\\\therefore \boxed{ \big|\big|v(t)\big|\big|=\sqrt{4t^2+(4)/(t^6) } }`

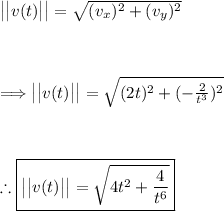
(d) Sketching the graph:

Now, let's address the sketch of the path of the particle and draw the velocity and acceleration vectors for t = 1.

To sketch the path of the particle, we need to look at the position vector r(t) = <t^2, 1/t^2> and see how it changes as t varies. Since t can take both positive and negative values, the path will be in both quadrants I and IV of the Cartesian plane.

For t = 1:

`r(t) = \Big < t^2, (1)/(t^2) \Big > \\\\\\\\\Longrightarrow r(t) = \Big < (1)^2, (1)/((1)^2) \Big > \\\\\\\\\therefore r(1) = \big < 1,1\big >`

So, at t = 1, the particle is located at the point (1, 1) in the Cartesian plane.

Now, let's find the velocity and acceleration vectors at t = 1:

`v(t) = \Big < 2t, -(2)/(t^3) \Big > \\\\\\\\\Longrightarrow v(1) = \Big < 2(1), -(2)/((1)^3) \Big > \\\\\\\\\therefore v(1)= \big < 2,-2\big >`

`a(t) = \Big < 2, (6)/(t^4) \Big > \\\\\\\\\Longrightarrow a(t) = \Big < 2, (6)/((1)^4) \Big > \\\\\\\\\therefore a(1)= \big < 2,6\big >`

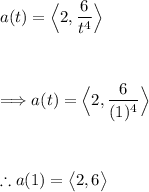
So, at t = 1:

Velocity vector (v) is <2, -2>.

Acceleration vector (a) is <2, 6>.

To draw these vectors on the sketch, plot the point (1, 1) and draw the vectors with their tails at this point. The vector <2, -2> represents the velocity, and the vector <2, 6> represents the acceleration. Make sure to label the vectors for clarity. Refer to the attached photo for the sketch.