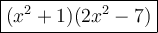Question

Hello,

I need help to understand the process on how to factor this equation. I have been trying to find different methods and for some reason I don't get it. Thank you in advance

`2x^4-5x^2-7`

Answer 1

To find :

• Factors of 2x⁴-5x²-7

Solution :

• 2x⁴-5x²-7

By splitting the middle term,

• 2x⁴-7x²+2x²-7
• x²(2x²-7) + 2x²-7
• (2x²-7)+x²-2x²-7
• (2x²-7)+x²+1(2x²-7)

Grouping the common factors,

• (x²+1)(2x²-7)

Therefore,(x²+1)(2x²-7) are the factors of the equation 2x⁴-5x²-7

Answer 2

`(x^2+1)(2x^2-7)`

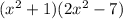
Explanation:

To factor the quartic expression 2x⁴ - 5x² - 7, we can substitute u = x² to turn the quartic into a quadratic in terms of u, then factor by grouping.

`\textsf{Let $u = x^2$}`

`\therefore u^2 = (x^2)^2 = x^4`

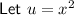
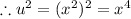
Rewrite the given expression in terms of u:

`2u^2-5u-7`

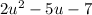
Now we have a quadratic expression, and can factor it in the usual way.

To factor a quadratic in the form ax² + bx + c, begin by finding two numbers that multiply to ac and sum to b.

In this case:

• 
  `a = 2`
• 
  `b = -5`
• 
  `c = -7`

Therefore:

`ac=2 \cdot -7=-14`

`b=-5`

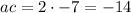
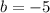
The two numbers that multiply to -14 and sum to -5 are
`\boxed{\sf -7 \;and \;2}`.

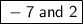Rewrite b as the sum of these two numbers:

`2u^2-7u+2u-7`

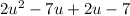
Factor the first two terms and the last two terms separately:

`u(2u-7)+1(2u-7)`

Factor out the common term (2u - 7):

`(u+1)(2u-7)`

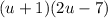
Substitute back u = x²:

`(x^2+1)(2x^2-7)`

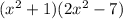
Therefore, the given expression factored is:

`\large\boxed{(x^2+1)(2x^2-7)}`