Question

Let 0° < a < 90°
Given: cos a=7/25
Find: sin a and cot a

Answer 1

You can use inverse trigonometry to solve this problem.

What is inverse trignometry?

Unlike regular trigonometry, where you use the angles measurements you are given to find the ratio/decimal of that angle, inverse trigonometry uses the ratios you are given from
`S(O)/(H)C(A)/(H)T(O)/(H)` to find the angle measurements.

You have been given this information:

cos (A) =
`(7)/(25)`

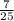
You do not have the angle measurement, however, you do have
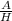`(A)/(H)`, the ratio of cosine (adjacent/hypothenuse), and interestingly enough two of the three parts of the pythagorean theorem equation.

To find sin a, first use the pythagorean theorem to find O, or the opposite leg of the triangle in
`S(O)/(H)`

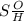
The Pythagorean Theorem is an equation used to find the lengths of the sides of a triangle: a² + b² = c²

Right now, you have c [25], the hypothenuse of the triangle, which is represented by H in
`S(O)/(H)C(A)/(H)T(O)/(H)`.

You also have the length of one side of the triangle: 7, represented by A in
`C(A)/(H)`

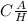
To find the other leg, plug in 7 and 25 into the the pythagorean theorem:

7² + b² = 25²

Now solve for b:

7² + b² = 25²

b²= 25² - 7²

b² = 625 - 49

b² = 576

b = √576 = 24

Now that you have b, you have O. Use inverse trigonometry to find sin a:

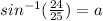`sin^(-1)((24)/(25))= a` = 73.7°

Now for cot a:

Cot A is the reciprocal of tangent or
`T(O)/(A)`

You have O and A from your previous problems

• O: 24 and A: 7

To find cot A, flip tangent's ratio
`(O)/(A)` to
`(A)/(O)` and plug your values in

`(A)/(O) = (24)/(7)`

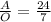
Now, use inverse trigonometry again and plug into your calculator:

`cot^(-1) ((24)/(7) )=A`

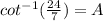
A= 16.3°

*please make sure your scientific calculator is in degrees before solving this problem*