Answer:
0.9825
Explanation:
The Magazine Mass Marketing Company has received 14 entries in its latest sweepstakes. They know that the probability of receiving a magazine subscription order with an entry form is 0.6.
To calculate the probability that more than 4 of the entry forms will include an order, we can model the given scenario as a binomial distribution.
Binomial distribution
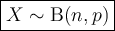
where:
- X is the random variable that represents the number of successes.
- n is the fixed number of independent trials.
- p is the probability of success in each trial.
Given the probability of receiving a magazine subscription order with an entry form is 0.6, and the number of entries is 14:
Therefore:

where the random variable X represents the number of entry forms that include a magazine subscription order.
To find the probability that more than 4 of the entry forms include a magazine subscription order, we need to find P(X ≥ 5).
The complement rule of probability states that the probability of an event occurring is equal to one minus the probability of that event not occurring. Therefore:
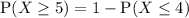
We can use a calculator to calculate P(X ≤ 4) using the binomial cumulative distribution function (cdf). Note that the binomial cdf on a calculator will give you the sum of all the binomial probabilities for values of your random variable less than or equal to a given number (i.e. P(X ≤ x)).
Inputting the values of n = 14, p = 0.6 and x = 4 into the binomial cdf we get:
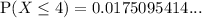
Therefore:
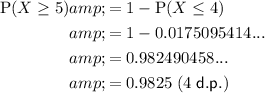
So the probability that more than 4 of the entry forms will include a magazine subscription order is 0.9825 (4 d.p.).