Question

Don’t understand this problem at all

Answer 1

The cost of a cheeseburger was $2.79.

The cost of an order of medium fries was $1.79.

Therefore, the Greens calculations were incorrect.

Explanation:

When visiting friends in a state that has no sales tax, two families went to a fast-food restaurant for lunch:

• The Browns bought 4 cheeseburgers and 3 medium fries for $16.53.
• The Greens bought 5 cheeseburgers and 4 medium fries for $21.11.

Using c for the cost of a cheeseburger and f for the cost of medium fries, we can write a system of equations that models the situation:

`\begin{cases}4c+3f=16.53\\5c+4f=21.11\end{cases}`

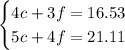
To determine if the Greens have calculated the cost of a cheesburger and an order of medium fries correctly, we can solve the system of equations by the method of elimination.

Multiply the first equation by 4 and multiply the second equation by 3 so that the coefficients of the terms in f are the same:

`4(4c+3f=16.53)\implies 16c+12f=66.12`

`4(5c+4f=21.11)\implies 15c+12f=63.33`

Subtract the second equation from the first to eliminate the terms in f:

`\begin{array}{crcccr}&16c&+&12f&=&66.12\\-&(15c&+&12f&=&63.33\\\cline{2-6}&c&&&=&2.79\end{array}`

Therefore, the cost of a cheeseburger was $2.79.

To find the cost of an order of medium fries (f), substitute the found value of c into one of the equations and solve for f:

`\begin{aligned}4(2.79)+3f&=16.53\\11.16+3f&=16.53\\11.16+3f-11.16&=16.53-11.16\\3f&=5.37\\3f / 3&=5.37/ 3\\f&=1.79\end{aligned}`

Therefore, the cost of an order of medium fries was $1.79.

This means that the Greens were incorrect in their calculation that each cheeseburger must cost $2.49 and each order of medium fries must cost $2.87 each.