Question

What is the GCF for -30xy^4,10x^4,90x^2y^3

Answer 1

GCF for -30xy^4, 10x^4, and 90x^2y^3 is 10x.

Explanation:

The greatest common factor (GCF) of two or more numbers is the largest number that is a factor of all of them.

For the question:

Monomials -30xy^4, 10x^4, and 90x^2y^3, we get the following:

`\sf 1st \;\: term: -30xy^4 = -2 * 3 * 5 * x * y * y * y*y`

`\sf 2nd \:\:Term =10x^4 = 2 * 5 * x * x * x * x`

`\sf 3rd \:\: term =90x^2y^3 = 2 * 3 * 3 * 5 * x * x * y * y * y`

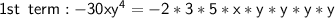
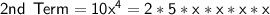
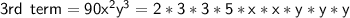
The prime factors that are common to all of the monomials are 2, 5, and x, so the GCF is 2 * 5 * x = 10x.

Therefore, the GCF for -30xy^4, 10x^4, and 90x^2y^3 is 10x.