Answer:
50626 ways with a probability of 0.77
Explanation:
If a coin is tossed once, there are two possible results - a head or a tail. i.e 2¹ = 2
If the coin is tossed twice, there are four possible results - 4 heads no tail, 4 tails no head, 1 head 3tails or 2 heads 2 tails. That is 2² = 4
If the coin is tossed thrice, there are eight possible results. That is 2³ = 8.
Now, if the coin is tossed 16 times, there are 2¹⁶ = 65536 likely results.
From these 16 tosses, let's calculate the number of ways of achieving or selecting 7, 8, 9, 10, 11, 12, 13 or 14 heads. We use the combination formula given as follows;
Cₙ, ₓ = n! ÷ [ (n-x)! (x)! ]
Where;
n = number of tosses
x = number of selection
number of ways of getting 7 heads;
n = 16
x = 7
=> C₁₆, ₇ = 16! ÷ [ (16-7)! (7)! ]
=> C₁₆, ₇ = 16! ÷ [ (9)! (7)! ]
=> C₁₆, ₇ = 11440
number of ways of getting 8 heads;
n = 16
x = 8
=> C₁₆, ₈ = 16! ÷ [ (16-8)! (8)! ]
=> C₁₆, ₈ = 16! ÷ [ (8)! (8)! ]
=> C₁₆, ₈ = 12870
number of ways of getting 9 heads;
n = 16
x = 9
=> C₁₆, ₉ = 16! ÷ [ (16-9)! (9)! ]
=> C₁₆, ₉ = 16! ÷ [ (7)! (9)! ]
=> C₁₆, ₉ = 11440
number of ways of getting 10 heads;
n = 16
x = 10
=> C₁₆, ₁₀ = 16! ÷ [ (16-10)! (10)! ]
=> C₁₆, ₁₀ = 16! ÷ [ (6)! (10)! ]
=> C₁₆, ₁₀ = 8008
number of ways of getting 11 heads;
n = 16
x = 11
=> C₁₆, ₁₁ = 16! ÷ [ (16-11)! (11)! ]
=> C₁₆, ₁₁ = 16! ÷ [ (5)! (11)! ]
=> C₁₆, ₁₁ = 4368
number of ways of getting 12 heads;
n = 16
x = 12
=> C₁₆, ₁₂ = 16! ÷ [ (16-12)! (12)! ]
=> C₁₆, ₁₂ = 16! ÷ [ (4)! (12)! ]
=> C₁₆, ₁₂ = 1820
number of ways of getting 13 heads;
n = 16
x = 13
=> C₁₆, ₁₃ = 16! ÷ [ (16-13)! (13)! ]
=> C₁₆, ₁₃ = 16! ÷ [ (3)! (13)! ]
=> C₁₆, ₁₃ = 560
number of ways of getting 14 heads;
n = 16
x = 14
=> C₁₆, ₁₄ = 16! ÷ [ (16-14)! (14)! ]
=> C₁₆, ₁₄ = 16! ÷ [ (2)! (14)! ]
=> C₁₆, ₁₄ = 120
Therefore, the total number of ways of achieving 7, 8, 9, 10, 11, 12, 13 or 14 heads is the sum of the results above. i.e
11440 + 12870 + 11440 + 8008 + 4368 + 1820 + 560 + 120 = 50626 ways
P(getting number of heads between 7 and 14 inclusive) = [number of ways of achieving 7, 8, 9, 10, 11, 12, 13 or 14 ] ÷ [total number of possible outcomes]
=
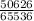
= 0.77