Question

Given o below, if GH and HJ are congruent, what is the measure of chord HJ?

• A. 9.2 units
O B. 8.6 units
O C. 7.8 units
O D. 17.2 units

Answer 1

B. 8.6 units

`\hrulefill`

Explanation:

The given diagram shows circle O with three radii, OG, OH and OJ.

The central angle formed by radii OG and OH is 82°.

The chord joining points G and H on the circumference of the circle measures 8.6 units.

The measure of a central angle of a circle is equal to the measure of its corresponding intercepted arc. Therefore, as m∠GOH = 82°, then:

`\sf \overset\frown{GH}= 82^(\circ)`

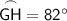
We are told that arcs
`\sf \overset\frown{GH}` and
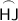`\sf \overset\frown{HJ}` are congruent.

Therefore, the measure of arc
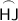`\sf \overset\frown{HJ}` is also 82°.

This means that the central angle formed by radii OH and OJ is also 82°.

The SAS (Side-Angle-Side) Congruency Theorem states that if two sides and the included angle in one triangle are congruent to two sides and the included angle in another triangle, the triangles are congruent.

Therefore, triangle GOH is congruent to triangle HOJ by SAS Congruency Theorem, which means that the chords are also congruent.

So the measure of chord
`\overline{\sf HJ}` is equal to the measure of chord
`\overline{\sf GH}`:

`\large\boxed{\overline{\sf HJ}=\sf 8.6\;units}`

Answer 2

B. 8.6 units

Explanation:

We Know

GH and HJ are congruent, meaning they are equal to each other. So, the answer is B. 8.6 units.