Question

What is the magnitude of -5+12i

Answer 1

13

Explanation:

sqrt( (-5)^2 + 12^2) =13

Answer 2

The magnitude of -5+12i is 13.

Explanation:

The magnitude of a complex number is its distance from the origin in the complex plane.

It can be calculated using the following formula:

`\boxed = √(a^2 + b^2)`

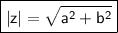
where z is the complex number, a is the real part of z, and b is the imaginary part of z.

In this case, the complex number is -5+12i, so the real part is -5 and the imaginary part is 12.

Plugging these values into the formula, we get:

`\sf |-5+12i| = √((-5)^2+ 12^2))=√(25 + 144)`

`\sf |-5+12i| =√(169)`

`\sf |-5+12i| = 13`

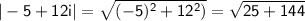
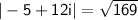
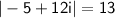
Therefore, the magnitude of -5+12i is 13.