Question

50 points Please help with just the last question

Calculate the ratio of the perimeter of the
dilated square to that of the original square. Calculate the ratio of the area of the area of the dilated square to that of the original square. Are these two ratios the same? Why
or why not? Explain your answer.

Answer 1

No, The two ratios are not the same.

Explanation:

Coordinates of the original square:

• A(-2, 2)
• B(2, 2)
• C(-2, -2)
• D(2, -2)

Area and perimeter of the original square:

Area =lenth*breadth = 4*4= 16 square units

Perimeter = sum of all sides = 4+4+4+4=16 units

we can find the distance by counting the box in the graph.

Coordinates of the dilated square:

• A'(-4, 4)
• B'(4, 4)
• C'(-4, -4)
• D'(4, -4)

Area and perimeter of the dilated square:

Area = 8*8=64 square units

Perimeter = 8+8+8+8=32 units

The ratio of the perimeter of the dilated square to that of the original square:

`\sf (32 )/( 16 )= 2`

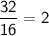
The ratio of the area of the dilated square to that of the original square:

`\sf ( 64 )/(16) = 4`

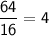
No, The two ratios are not the same. The ratio of the perimeter is 2, while the ratio of the area is 4.

This is because the perimeter of a shape is a linear measurement, while the area of a shape is a quadratic measurement.

When a shape is dilated by a scale factor of 2, the perimeter is multiplied by 2, but the area is multiplied by 4.

In other words, the perimeter of a shape is directly proportional to the scale factor, while the area of a shape is directly proportional to the square of the scale factor.