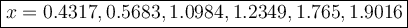Question

NO LINKS!! URGENT HELP PLEASE!!

Please help me with this solution part 3​

Answer 1

d) 0.43172, 0.568, 1.0984, 1.235, 1.765, 1.9016

`\hrulefill`

Explanation:

Given equation:

`5 \sin(3\pi x) + 8 = 4`

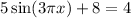
To find the solutions to the given equation in the interval 0 ≤ x ≤ 2 radians, first isolate the sine term and then solve for x.

Isolate the sine term by subtracting 8 from both sides and then dividing both sides of the equation by 5:

`\begin{aligned}5 \sin(3\pi x) + 8 &= 4\\\\5 \sin(3\pi x) &= -4\\\\\sin(3\pi x) &= -(4)/(5)\\\\\end{aligned}`

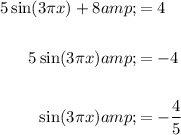
Solve for 3πx by taking the arcsine of both sides of the equation, remembering that the sine function has a periodicity of 2π and is negative in quadrants III and IV.

`\begin{aligned}\arcsin \left(\sin(3\pi x)\right)&= \arcsin \left(-(4)/(5)\right)\\\\3 \pi x&=-0.927295218...+2\pi n, \pi+0.927295218...+2\pi n\end{aligned}`

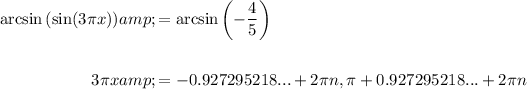
Divide both sides of the equation by 3π to solve for x:

`\begin{aligned}(3 \pi x)/(3 \pi)&=(-0.927295218...+2\pi n)/(3\pi), (\pi+0.927295218...+2\pi n)/(3 \pi)\\\\x&=-0.098389078...+(2)/(3)n, 0.43172241...+(2)/(3)n\end{aligned}`

To find the solutions for x that are in the given interval 0 ≤ x ≤ 2, add integer multiples of 3/2 to the found solutions:

`x=-0.098389078...+(2)/(3)=0.5683`

`x=-0.098389078...+2\left((2)/(3)\right)=1.2349`

`x=-0.098389078...+3\left((2)/(3)\right)=1.9016`

`x=0.4317`

`x=0.43172241...+(2)/(3)=1.0984`

`x=0.43172241...+2\left((2)/(3)\right)=1.7651`

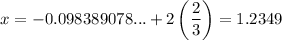
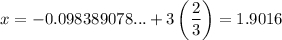
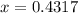
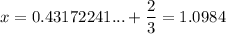
Therefore, the solutions in the given interval are:

`\large\boxed{x=0.4317, 0.5683, 1.0984, 1.2349, 1.765, 1.9016}`