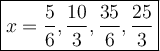Question

NO LINKS!! URGENT HELP PLEASE!!
Please help me with this solution part 2​

Answer 1

`\textsf{b)}\quad (5)/(6),(10)/(3),(35)/(6),(25)/(3)`

`\hrulefill`

Explanation:

Given equation:

`12\tan\left((2\pi)/(5)x\right)=12√(3)`

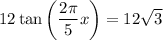
To find the solutions to the given equation in the interval 0 ≤ x ≤ 10 radians, first isolate the tangent term and then solve for x.

Isolate the tangent term by dividing both sides of the equation by 12:

`\begin{aligned}12\tan\left((2\pi)/(5)x\right)&=12√(3)\\\\\tan\left((2\pi)/(5)x\right)&=√(3)\end{aligned}`

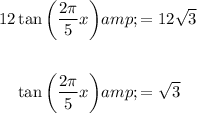
Solve for 2πx/5 by taking the arctan of both sides of the equation, remembering that the tangent function has a periodicity of π:

`\begin{aligned}\arctan\left(\tan\left((2\pi)/(5)x\right)\right)&=\arctan√(3)\\\\(2\pi)/(5)x&=(\pi)/(3)+\pi n\end{aligned}`

Multiply both sides of the equation by 5/2π to solve for x:

`\begin{aligned}(2\pi)/(5)x \cdot (5)/(2\pi)&=(\pi)/(3)\cdot (5)/(2\pi)+\pi n\cdot (5)/(2\pi)\\\\x&=(5)/(6)+(5)/(2)n\end{aligned}`

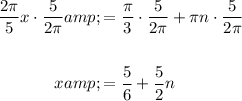
To find the solutions for x that are in the given interval 0 ≤ x ≤ 10, add integer multiples of 5/2 to the found solution:

`x=(5)/(6)`

`x=(5)/(6)+(5)/(2)=(10)/(3)`

`x=(5)/(6)+2\left((5)/(2)\right)=(35)/(6)`

`x=(5)/(6)+3\left((5)/(2)\right)=(25)/(3)`

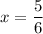
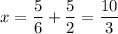
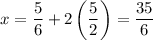
Therefore, the solutions in the given interval are:

`\large\boxed{x =(5)/(6),(10)/(3),(35)/(6),(25)/(3)}`