Question

NO LINKS!! URGENT HELP PLEASE!!

Please help me with this solution Part 5​

Answer 1

c) t = 0.1176, 0.7459, 1.3742

`\hrulefill`

Explanation:

To find the solutions to the equation 3 tan(5t) = 2 in the interval 0 ≤ t ≤ π/2 radians, first isolate the tangent term and then solve for t.

Isolate the tangent term by dividing both sides of the equation by 3:

`\begin{aligned}3 \tan (5t)&=2\\\\\tan(5t)&=(2)/(3)\end{aligned}`

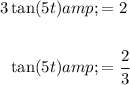
Solve for 5t by taking the arctan of both sides of the equation, remembering that the tangent function has a periodicity of π:

`\begin{aligned}\arctan\left(\tan (5t)\right)&=\arctan\let((2)/(3)\right)\\\\5t&=0.5880026...+\pi n\end{aligned}`

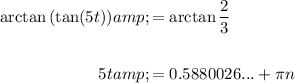
Finally, divide both sides of the equation by 5 to solve for t:

`\begin{aligned}(5t)/(5)&=(0.5880026...)/(5)+(\pi n)/(5)\\\\t&=0.11760052...+(\pi)/(5) n\end{aligned}`

The given interval is 0 ≤ t ≤ π/2 which is approximately 0 ≤ t ≤ 1.5708.

Therefore, to find the solutions for t that are in the given interval, add integer multiples of π/5 to the found solution:

`t=0.1176`

`t=0.1176+(\pi)/(5)=0.7459`

`t=0.1176+(2\pi)/(5)=1.3742`

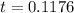
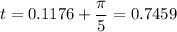
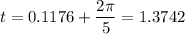
Therefore, the solutions of 3tan(5t) = 2 in the given interval are:

`\large\boxed{t=0.1176, 0.7459, 1.3742}`