Question

NO LINKS!! URGENT HELP PLEASE!!

Please help me with this problem.

Answer 1

your answer will be see cuz they say a particular species of so many has an average weight weight of 57 IPS or your aunt is going to be

1. C

Answer 2

c) Do not reject the null hypothesis; these fish are not larger than usual.

Explanation:

A particular species of salmon has an average weight of 57 lbs, with a standard deviation of 6.3 lbs. Assuming the weight, X, is normally distributed:

`X\sim \text{N}(\mu, \sigma^2)=X\sim \text{N}(57,6.3^2)`

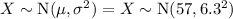
Researchers studying salmon in a particular river find that in a sample of 45 fish, the average weight is 58.5 lbs.

To determine what the researchers should do, we need to perform a hypothesis test to assess whether the sample average weight of 58.5 lbs is significantly different from the population average weight of 57 lbs.

Let μ be the mean weight of salmon (in pounds).

We are testing to see if the mean weight has increased, so this is a one-tailed test. Therefore, the hypotheses are:

• Null hypothesis H₀: μ = 57
• Alternative hypothesis H₁: μ > 57

We have not been given a significance level, so we will assume it is 5%.

Therefore, α = 0.05.

`\boxed{\begin{minipage}{10.2cm}If $X \sim \text{N}(\mu,\sigma^2)$, then $\overline{X} \sim \text{N}\left(\mu,(\sigma^2)/(n)\right) \implies Z=\frac{\overline{X}-\mu}{\sigma / √(n)} \sim \text{N}(0,1)$\\\\\\Then the value of the test statistic will be: \quad $z=\frac{\overline{x}-\mu}{\sigma / √(n)}$\\\end{minipage}}`

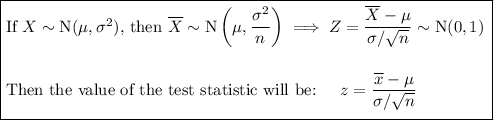
The sample mean
`\overline{x}` is 58.5 where n = 45.

Therefore, the test statistic is:

`z=(58.5-57)/(6.3/ √(45))=(5√(5))/(7)\approx1.59719141...`

This is a one-tailed test and values more likely to occur under H₁ are at the higher end of the distribution. Therefore, we need to find the critical value, z, such that P(Z > z) = 0.05.

Using a calculator, P(Z ≤ z) = 0.95 for z = 1.645.

So the critical region is Z > 1.645.

Since 1.597 < 1.645, the result does not lie in the critical region and is not significant. Therefore, there is insufficient evidence at the 5% level of significance to reject H₀ in favour of the alternative hypothesis that the mean salmon weight has gone up.