Question

PLEASE ANSWER QUICKLY

Answer 1

The first option, I_z = (1/3)ML²

Step-by-step explanation:

To compute the moment of inertia (I_z) of the thin rod about the z-axis, we'll use the given expression:

`\rightarrow I_z = \displaystyle \int {(x^2+y^2)\rho} \, dV`

Given that dV = dx and the constant mass density ρ = M / L, we can rewrite the expression as:

`\Longrightarrow I_z =\displaystyle \int {\Big[(x^2+y^2)\Big((M)/(L) \Big)\Big]} \, dx`

Now, let's consider the geometry of the thin rod. Since it is lying along the x-axis, its y-coordinate is always zero. Therefore, y = 0 for all points along the rod.

Now the expression becomes:

`\Longrightarrow I_z =\displaystyle \int {\Big[(x^2+(0)^2)\Big((M)/(L) \Big)\Big]} \, dx\\\\\\\\\Longrightarrow I_z =\displaystyle \int {\Big[(x^2)\Big((M)/(L) \Big)\Big]} \, dx\\\\\\\\\Longrightarrow I_z =(M)/(L)\displaystyle \int {(x^2)} \, dx`

Integrating x² with respect to x gives us:

`\Longrightarrow I_z =(M)/(L) \Big((1)/(3)x^3 \Big) + C`

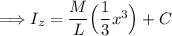
Now, we need to evaluate this expression at the limits of the rod's length, from 0 to L:

`\Longrightarrow I_z =\Big[(M)/(L) \Big((1)/(3)x^3 \Big) + C \Big]\limits^L_0\\\\\\\\\Longrightarrow I_z =\Big[(M)/(L) \Big((1)/(3)(L)^3 \Big) + C \Big]-\Big[(M)/(L) \Big((1)/(3)(0)^3 \Big) + C \Big]\\\\\\\\\Longrightarrow I_z =\Big[(M)/(L) \Big((1)/(3)(L)^3 \Big) + C \Big]-\Big[0 + C \Big]\\\\\\\\\Longrightarrow I_z =M \Big((1)/(3)(L)^2 \Big)\\\\\\\\\therefore \boxed{\boxed{I_z = (1)/(3)ML^2 }}`

Thus, the correct answer is the first option. The moment of inertia of the thin rod about the z-axis is (1/3)ML².

`\hrulefill`

Additional information:

Moment of Inertia (I): The moment of inertia measures an object's resistance to rotational motion about a particular axis. For a continuous object like the rod in this question, it is calculated using integration, as shown above.

Mass Density (ρ): Mass density is defined as the mass per unit volume of a substance. In this case, the mass density ρ = M / L represents the mass per unit length of the rod.

Integration: Integration is a fundamental concept in calculus used to find the area under a curve or the accumulation of a quantity. In this context, it helps us find the moment of inertia of the thin rod by integrating the infinitesimal elements of the rod along its length.

Limits of Integration: The limits of integration are the starting and ending points of the integral. In this problem, we integrate from 0 to L because we want to sum up the contributions of infinitesimal elements along the entire length of the rod.

Constant Mass Density: The assumption of a constant mass density means that the mass distribution along the rod is uniform, and the mass per unit length remains the same throughout the rod. This simplifies the calculation of the moment of inertia.