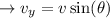Question

Need solution please​

Answer 1

The problem is about projectile motion, which is the motion of an object that is thrown or launched into the air. To solve this problem, we need to use the following equations:

- Horizontal displacement: x = v_x * t

- Vertical displacement: y = v_y * t - 0.5 * g * t^2

- Initial horizontal velocity: v_x = v_0 * cos(theta)

- Initial vertical velocity: v_y = v_0 * sin(theta)

Where x and y are the horizontal and vertical displacements, v_x and v_y are the horizontal and vertical velocities, v_0 is the initial velocity, theta is the launch angle, t is the time, and g is the acceleration due to gravity (9.8 m/s^2).

To find the height at which the baseball hits the wall, we need to find the time when the horizontal displacement is equal to 6 meters, and then plug that time into the vertical displacement equation. Here are the steps:

- Find the initial horizontal velocity: v_x = 8 * cos(45) = 5.66 m/s

- Find the time when x = 6: 6 = 5.66 * t -> t = 1.06 s

- Find the initial vertical velocity: v_y = 8 * sin(45) = 5.66 m/s

- Find the vertical displacement when t = 1.06: y = 5.66 * 1.06 - 0.5 * 9.8 * 1.06^2 = 2.48 m

Therefore, the height at which the baseball hits the wall is **2.48 m**. C

Answer 2

Option (c) is correct, h = 2.48 m

Step-by-step explanation:

To determine the height at which the baseball hits the wall, we can use the equations of motion and principles of projectile motion. The key concept involved here is projectile motion.

`\hrulefill`

Let's solve step-by-step:

Step 1: Split up the initial velocity into its components.

Given:

• v = 8 m/s

• θ = 45°

Horizontal component:

`v_x=v\cos(\theta)\\\\\\\\\Longrightarrow v_x=(8)\cos(45 \textdegree)\\\\\\\\\therefore v_x = 4\sqrt2 \ m/s`

Vertical component:

`v_y=v\sin(\theta)\\\\\\\\\Longrightarrow v_y=(8)\sin(45 \textdegree)\\\\\\\\\therefore v_y = 4\sqrt2 \ m/s`

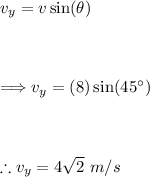
Step 2: Find the time the baseball is in the air.

Let's use the horizontal components and the third kinematic equation to find the time, t.

Given:

• Δx = 6 m
• v_x = 4√2 m/s
• a_x = 0 m/s² (v_x remains constant throughout it's flight)

Substitute in our values and solve for "t":

`\Delta \vec x=\vec v_xt+(1)/(2)\vec a_xt^2\\\\\\\\\Longrightarrow 6=(4\sqrt2)t+(1)/(2) (0)t^2\\\\\\\\\Longrightarrow 6=(4\sqrt2)t\\\\\\\\\Longrightarrow t=(6)/(4\sqrt2) \\\\\\\\\therefore t = (3\sqrt2)/(4) \ s`

Step 3: Finding the height, h.

Now we can use the vertical components and the third kinematic equation to find the height, h.

Given:

• v_y = 4√2 m/s
• a_y = -9.8 m/s² (acceleration due to gravity)
• t = (3√2)/4 s

`\Delta \vec y=\vec v_yt+(1)/(2)\vec a_yt^2\\\\\\\\\Longrightarrow \Delta \vec y= (4√(2) )((3√(2) )/(4))+(1)/(2)(-9.8)((3√(2) )/(4) )^2\\\\\\\\\Longrightarrow \Delta \vec y= 6-5.5125\\\\\\\\\therefore \Delta \vec y= 0.4875 \ m`

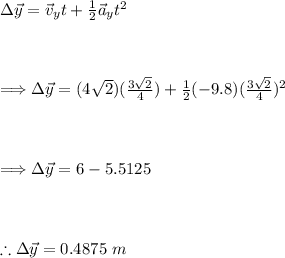
We can find "h" as follows:

`\Longrightarrow h= \Delta \vec y +2\\\\\\\\\Longrightarrow h= 0.4875 +2\\\\\\\\\therefore \boxed{h=2.4875 \ m}`

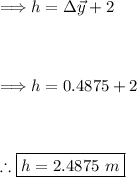
Thus, option (c) is the correct choice.

`\hrulefill`

Additional Information:

Projectile Motion: Projectile motion refers to the motion of an object (the projectile) that is thrown or projected into the air, subject only to the force of gravity. In this case, the baseball is a projectile, and it moves in a two-dimensional plane (horizontal and vertical) under the influence of gravity.

Equations of Motion: These are the set of equations that describe the motion of an object under constant acceleration. They are used to relate the initial velocity, final velocity, acceleration, time, and displacement of an object. The equations differ for horizontal and vertical motion, as motion in each direction is independent of the other.

The four kinematic equations are given as follows:

`\boxed{\left\begin{array}{ccc}\text{\underline{The 4 Kinematic Equations:}}\\\\1. \ \vec v_f=\vec v_0+\vec at\\\\2. \ \Delta \vec x=(1)/(2)(\vec v_f-\vec v_0)t\\\\3. \ \Delta \vec x=\vec v_0t+(1)/(2)\vec at^2\\\\ 4. \ \vec v_f^2=\vec v_0^2+2\vec a \Delta \vec x \end{array}\right}`

Splitting velocity into it's components: Splitting velocity into its components is a common concept used in physics, especially when dealing with motion in two or three dimensions. When an object is moving in a two-dimensional plane, like in the case of projectile motion, its velocity can be broken down into two perpendicular components: horizontal and vertical.

Consider a velocity vector v with an angle θ (theta) with respect to the horizontal axis, as shown in the attached image:

v is the magnitude (speed) of the velocity vector.v_x is the horizontal component of the velocity.v_y is the vertical component of the velocity.

To calculate these components, we use trigonometric functions. Based on the angle θ, we can express v_x and v_y in terms of v as follows:

Horizontal component:

`\rightarrow v_x=v\cos(\theta)`

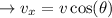
Vertical component:

`\rightarrow v_y=v\sin(\theta)`