Question

Im confused on how to do this someone help pls!

Answer 1

47.1784 cm² using the given areas in the question.

47.1785 cm² using the correctly calculated areas (see below).

Explanation:

The area of the shaded region can be found by subtracting the area of the isosceles triangle from the area of a sector of the circle.

The formula for the area of a sector of a circle is:

`\boxed{\textsf{Area of a sector of a circle}=\left((\theta)/(360^(\circ))\right) \pi r^2}`

where r is the radius, and the angle θ is measured in degrees.

The radius of the circle is 8 cm and the central angle is 129°.

Therefore, to find the area of the sector, substitute r = 8 and θ = 129° into the formula:

`\begin{aligned}\textsf{Sector Area}&=\left((129^(\circ))/(360^(\circ))\right) \pi \cdot 8^2\\\\&=(129)/(360)\pi \cdot 64\\\\&=(344)/(15)\pi\\\\&=72.0471915...\\\\&=72.0472\; \sf cm^2\;(4\;d.p.)\end{aligned}`

Therefore, the area of the sector is 72.0472 cm², rounded to four decimal places.

The formula for the area of an isosceles triangle is:

`\boxed{\textsf{Area of an isosceles triangle}=(1)/(2)s^2\sin\theta}`

where s is measure of the leg, and θ is the angle of the apex.

The leg of the triangle is 8 cm and the apex angle is 129°.

Therefore, to find the area of the isosceles triangle, substitute s = 8 and θ = 129° into the formula:

`\begin{aligned}\textsf{Triangle Area}&=(1)/(2)\cdot 8^2 \cdot \sin 129^(\circ)\\\\&=(1)/(2)\cdot 64 \cdot \sin 129^(\circ)\\\\&=32\sin 129^(\circ)\\\\&=24.8686707666...\\\\&=24.8687\; \sf cm^2\end{aligned}`

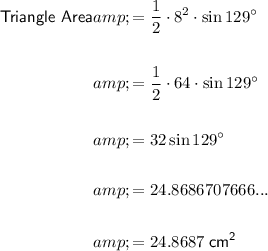
Therefore, the area of the triangle is 24.8687 cm², rounded to four decimal places.

Please note that the given area of the triangle is incorrect in the question.

To calculate the area of the shaded region, subtract the area of the triangle from the area of the sector:

`\begin{aligned}\textsf{Area of the Shaded Region}&=\sf Area_(sector)-Area_(triangle)\\\\&=(344)/(15)\pi-32\sin 129^(\circ)\\\\&=47.1785207...\\\\&=47.1785\; \sf cm^2\;(4\;d.p.)\end{aligned}`

If we use the given areas from the question, (noting that the area of the triangle is incorrect), the area of the shaded region is:

`72.0472 - 24.8688 = 47.1784 \; \sf cm^2\;(4\;d.p.)`

Answer 2

Area of shaded region =
`\boxed{\sf 47.1784 }` cm²

Explanation:

We can easily find the area of the shaded region by subtracting the Triangle area from Sector Area.

We have,

Triangle Area = 24.8688 cm²

Sector Area = 72.0472 cm²
Now,

Area of shaded region = Sector Area - Triangle Area

Area of shaded region = 72.0472 - 24.8688

Area of shaded region = 47.1784 cm²
Therefore, the Area of the shaded region =
`\boxed{\sf 47.1784 }` cm²