Question

Show the work that led to your

answers in each part. An object is thrown up from a height of 12 feet at a velocity of 36
feet/sec.

a. Find an equation for the velocity v(t) as a function of time t. Because of gravity, the acceleration is constant and acceleration a(t) =
v'(t) = dv/dt = -32ft/sec^2

b. Find an equation for the height s(t) as a function of time t.

c. What was the maximum height of the object?

d. How fast was the object traveling downward
when it hit the ground? Give your answer to 3
decimal places. Show the work.

Answer 1

Step-by-step explanation:

a. Use a = dv/dt.

`(dv)/(dt)=-32\\ dv=-32dt`

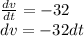
Integrate both sides:

`\int\limits^v_(36) {} \, dv=\int\limits^t_0 {-32} \, dt \\v-36=-32t\\v=36-32t`

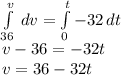
b. Use v = ds/dt.

`(ds)/(dt)=36-32t\\ ds=(36-32t)dt`

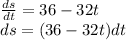
Integrate both sides:

`\int\limits^s_(12) {} \, ds=\int\limits^t_0 {(36-32t)} \, dt\\ s-12=36t-16t^2\\ s=-16t^2+36t+12`

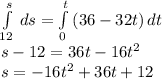
c. At the maximum height, v = 0.

`0=36-32t\\t=1.125 s`

The height of the object at this time is:

`s=-16(1.125)^2+36(1.125)+12\\s=32.25ft`

d. When the object reaches the ground, s = 0.

`0=-16t^2+36t+12\\0=4t^2-9t-3\\t=(9\pm√((-9)^2-4(4)(-3)) )/(2(4)) \\t=(9\pm√(129) )/(8)\\t=2.545 s`

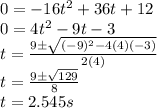
At that time, the velocity of the object is:

`v=36-32(2.545)\\v=-45.431 ft/s`