Question

A science test, which is worth 100 points, consists of 24 questions. Each question is worth either 3 points or 5

points. If x is the number of 3-point questions and y is the number of 5-point questions, the system shown
represents this situation.
x + y = 24
3x + 5y = 100
What does the solution of this system indicate about the questions on the test?
O The test contains 4 three-point questions and 20 five-point questions.
The test contains 10 three-point questions and 14 five-point questions.
The test contains 14 three-point questions and 10 five-point questions.
The test contains 20 three-point questions and 8 five-point questions.

Answer 1

B) The test contains 10 three-point questions and 14 five-point questions.

Explanation:

Given system of equations:

`\begin{cases}x + y = 24\\3x + 5y = 100\end{cases}`

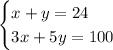
To find the solution of the given system of equations, we can use the method of substitution.

Rearrange the first equation to isolate y:

`\begin{aligned}x+y&=24\\x+y-x&=24-x\\y&=24-x\end{aligned}`

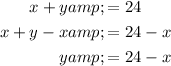
Substitute the expression for y into the second equation and solve for x:

`\begin{aligned}3x+5(24-x)&=100\\3x+120-5x&=100\\120-2x&=100\\120-2x-120&=100-120\\-2x&=-20\\-2x / -2&=-20 / -2\\x&=10\end{aligned}`

Substitute the found value of x into the rearranged first equation and solve for y:

`\begin{aligned}y&=24-10\\y&=14\end{aligned}`

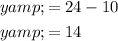
Therefore, the solution to the system of equations is:

• 
  `x = 10`
• 
  `y = 14`

Given that x is the number of 3-point questions and y is the number of 5-point questions, the solution indicates that the test contains 10 three-point questions and 14 five-point questions.