Question

A 0.24 kg mass is held against a compressed spring with a spring constant of 2,549 N/m. The mass is initially at rest upon a horizontal surface and the spring force is directed parallel to the plane of the surface. If the coefficient of kinetic friction is 0.661, with what speed does the mass leave contact with

the spring if the spring is initially compressed by 0.055 m?

Answer 1

Approximately
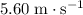`5.60\; {\rm m\cdot s^(-1)}` (assuming that
`g = 9.81\; {\rm N \cdot kg^(-1)}`.)

Step-by-step explanation:

To find the velocity of the mass right before it leaves the spring, start by considering how energy is converted in this process. As the spring decompresses, part of the elastic potential energy (
`\text{EPE}`) in the spring is lost as a result of friction. The rest of
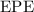`\text{EPE}\!` would be converted into the kinetic energy (
`\text{KE}`) of the mass:

`(\text{initial EPE}) = (\text{final KE}) + (\text{energy loss to friction})`.

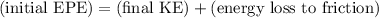To find the kinetic energy of the mass, it will be necessary to find the value of both the initial
`\text{EPE}` in the spring and the amount of energy lost as a result of friction.

• The initial
  `\text{EPE}` in the spring can be found from the spring constant and the displacement of the spring.
• To find the amount of energy lost as a result of friction, start by finding the normal force between the two surfaces. Multiply normal force by the coefficient of kinetic friction to find the magnitude of friction. Multiply the magnitude of friction by the distance travelled to find the amount of energy lost as a result of friction.

Subtract the amount of energy lost as a result of friction from the initial
`\text{EPE}` of the spring to find the
`\text{KE}` of the mass right before leaving the spring. The speed of the mass can be directly found from
`\text{KE}\!`.

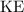When a spring with spring constant
`k` is compressed by a displacement of
`x`, the elastic potential energy (
`\text{EPE}`) stored in the spring would be:

`\displaystyle \text{EPE} = (1)/(2)\, k\, x^(2)`.

Given that the surface is horizontal, the normal force between the mass and the surface would be equal to the weight of the mass
`m = 0.24\; {\rm kg}`:

`\displaystyle (\text{normal force}) = (\text{weight}) = m\, g`,

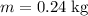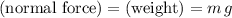Where
`g = 9.81\; {\rm N\cdot kg^(-1)}` is the gravitational field strength.

Since the mass is already moving, multiply the normal force by the coefficient of kinetic friction
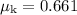`\mu_{\text{k}} = 0.661` to find the magnitude of friction on this mass:

`\begin{aligned}& (\text{kinetic friction}) \\ &= \mu_{\text{k}}\, (\text{normal force}) \\ &= \mu_{\text{k}} \, m\, g\end{aligned}`.

Multiply the magnitude of friction
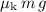`\mu_{\text{k}}\, m\, g` by distance
`x = 0.055\; {\rm m}` to find the amount of energy lost as a result of friction:
`\mu_{\text{k}}\, m\, g\, x`.

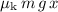Subtract the amount of energy lost as a result of friction from the initial
`\text{EPE}` of the spring to find the
`\text{KE}` of the mass right before leaving the spring:

`\begin{aligned} (\text{final KE}) &= (\text{initial EPE}) - (\text{energy loss to friction}) \\ &= (1)/(2)\, k\, x^(2) - \mu_{\text{k}}\, m\, g\, x\end{aligned}`.

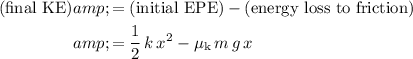At the same time,
`(\text{KE}) = (1/2)\, m\, v^(2)` where
`m` is the mass and
`v` is the speed. Equate the two expressions for
`(\text{KE})` to obtain:

`\displaystyle (1)/(2)\, m\, v^(2) = (1)/(2)\, k\, x^(2) - \mu_{\text{k}} \, m\, g\, x`.

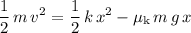Simplify this equation and solve for velocity
`v` to obtain:

`\begin{aligned}m\, v^(2) = k\, x^(2) - 2\, \mu_{\text{k}}\, m\, g\, x\end{aligned}`.

`\displaystyle v^(2) = (k\, x^(2))/(m) - 2\, \mu_{\text{k}}\, g\, x`.

`\begin{aligned} v &= \sqrt{(k\, x^(2))/(m) - 2\, \mu_{\text{k}}\, g\, x} \\ &= \sqrt{((2549)\, (0.055)^(2))/((0.24)) - 2\, (0.661)\, (9.81)\, (0.055)}\; {\rm m\cdot s^(-1)} \\ &\approx 5.60\; {\rm m\cdot s^(-1)}\end{aligned}`.

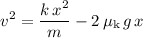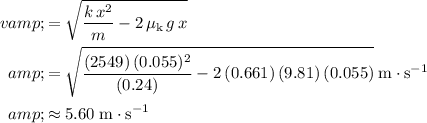In other words, the speed of the mass would be approximately
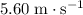`5.60\; {\rm m\cdot s^(-1)}` right before leaving the spring.