Question

Hello! I'm stuck on creating equations for the problem described. I recognize the pattern goes up x2 each day, but I'm not sure how else to figure out on setting up the equations. Thank you so much!: A student decides she wants to save money to buy a used car, which costs $2600. She comes up

with what she thinks is a very modest savings plan. She decides to save 2 cents the first day and

double the amount she saves each day thereafter. On the second day she plans to save 4 cents, on

the third day, 8 cents, and so on. 1. Write an expression that represents the amount saved on day n 2. Write an expression that represents the total amount saved by day n (including day n) 3. ) Determine how long it will take her to save enough money to buy the car.

Answer 1

17 days

Explanation:

It is a geometry sequence & series question:

the amount saved on day n:

Un = 2ⁿ

the total amount saved by day n:

`Sn=(a(r^n-1))/(r-1)`

• the first saving is 2cents = $0.02 ⇒ a = 0.02
• subsequent amount is 2x previous amount ⇒ r = 2

`Sn=(0.02(2^n-1))/((2-1))`

`Sn=0.02(2^n-1)`

how long it will take her to save enough money to buy the car:

Sn = 2600

0.02(2ⁿ - 1) = 2600

2ⁿ - 1 = 2600 ÷ 0.02

2ⁿ = 130000

n = ₂ log 130000

=
`(log\ 130000)/(log\ 2)`

= 17 days

Answer 2

Problem 1

We have the geometric sequence: 2, 4, 8, 16, 32, 64, ...

The first term is a = 2. The common ratio is r = 2 to represent each term doubling.

The geometric nth term formula is:

`a_n = a*(r)^(n-1)\\\\a_n = 2*(2)^(n-1)\\\\`

Therefore, the number of cents saved on day n would be
`2*(2)^(n-1)`

For example, if it is day 5 then the student will have
`2*(2)^(n-1) = 2*(2)^(5-1) = 2*(2)^4 = 2*16 = 32` cents saved up for that day only.

Compare it to the list mentioned above. This does not include the previous amount of money saved from the previous days.

=========================================

Problem 2

The previous problem handled just how much is saved on day n, and doesn't include the earlier amounts saved.

This time we'll include the previous days.

Use the geometric series formula

`S_n = (a*(1-r^n))/(1-r)`

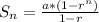
where a = 2 and r = 2 as mentioned before.

The
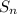`S_n` is the total amount saved on day n.

Let's plug in a = 2 and r = 2, then simplify

`S_n = (a*(1-r^n))/(1-r)\\\\S_n = (2*(1-2^n))/(1-2)\\\\S_n = (2*(1-2^n))/(-1)\\\\S_n = -2*(1-2^n)\\\\`

Other forms are possible.

--------

Let's test this formula out.

The first four days has these savings values: 2,4,8,16

Those add to 2+4+8+16 = 6+24 = 30

The student saves a total of 30 cents on day 4.

Plug n = 4 into the
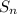`S_n` formula to get...

`S_n = -2*(1-2^n)\\\\S_4 = -2*(1-2^4)\\\\S_4 = -2*(1-16)\\\\S_4 = -2*(-15)\\\\S_4 = 30\\\\`

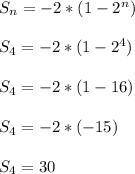
We conclude that at the end of day 4, the student will have 30 cents total saved up when combining all four days together.

This example verifies the formula works when n = 4. I'll let you try other values of n out. A spreadsheet program is handy to keep track of everything.

--------

To summarize, the answer to problem 2 is the expression
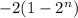`-2(1-2^n)` although that expression can be rewritten.

=========================================

Problem 3

2600 dollars = 2600*100 = 260,000 cents

The student needs to save up for 260,000 cents or higher.

Set this value equal to the right-hand-side of the
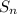`S_n` formula so we can solve for n.

Because n is in the exponent, we'll need a logarithm. I find the saying "if the exponent is in the trees then we log it down" to be a helpful memorization device.

Why are logs used? Because of the key log rule that log(A^B) = B*log(A) so we can pull down the exponent.

Here's what the steps look like to solve for n.

`S_n = -2*(1-2^n)\\\\260000 = -2*(1-2^n)\\\\260000/(-2) = 1-2^n\\\\-130000 = 1-2^n\\\\1-2^n=-130000\\\\-2^n=-130000-1\\\\`

`-2^n=-130001\\\\2^n=130001\\\\\log(2^n)=\log(130001)\\\\n\log(2)=\log(130001)\\\\n=\log(130001)/\log(2)\\\\n\approx16.988163195302\\\\n\approx17\\\\`

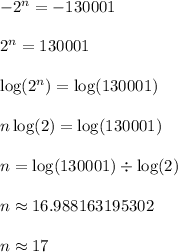
She'll need 17 days to save up the 260,000 cents (aka $2600) needed.

--------

As a check,

`S_n = -2*(1-2^n)\\\\S_(16) = -2*(1-2^(16))\\\\S_(16) = 131,070\\\\`

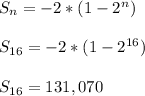
which comes up short of the goal

While,

`S_n = -2*(1-2^n)\\\\S_(17) = -2*(1-2^(17))\\\\S_(17) = 262,142\\\\`

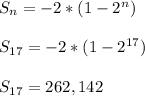
which goes over the goal. It's better to go over than come up short.