Question

PLS HELP! 40 points

A farmhouse shelters 20 animals. Some are cows, and some are ducks. Altogether there are 64 legs. How many cows are there?

Answer 1

12 cows

Explanation:

We can represent the number of cows in the variable c and the number of ducks in the variable d.

Using these variables, we can create a system of equations using the given information. We know that there are:

- 20 animals in total; therefore:

(number of cows) + (number of ducks) = 20, and using the variables:

`c + d = 20`

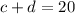
- 64 legs in total; therefore:

4(number of cows) + 2(number of ducks) = 64, and using the variables:

`4c + 2d = 64`

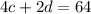
This is because cows have 4 legs, and ducks have 2 legs.

We can solve this system of equations using elimination with the following format: (second equation) - 2(first equation)

`\text{ }\ 4c + 2d = 64 \\ \underline{-2(c + d = 20)}`

↓↓↓

`\text{ }\ \ \, 4c + 2d = 64 \\ \underline{-(2c + 2d = 40)}`

`2c + 0 = 24`

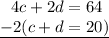
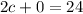
↓ dividing both sides by 2 to solve for
`c`

`c = 12`

So, there are 12 cows.