Answer: 94
Work Shown:
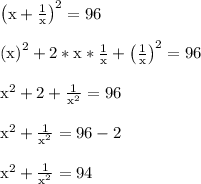
Step-by-step explanation:
I used the rule (A+B)^2 = A^2+2AB+B^2 on the second step. Conveniently the x terms cancel when computing the 2AB portion. This yields a constant that can be moved over to the other side to isolate the
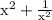 portion.
portion.
A longer method would be to solve for x to get four approximate roots. Those roots are
x = -0.10315
x = 0.10315
x = -9.6948
x = 9.6948
Then plug one of those roots into

Let's try x = -0.10315
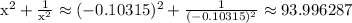 which is really close to 94. There's rounding error going on. Use more decimal digits in each root to get a more accurate value for
which is really close to 94. There's rounding error going on. Use more decimal digits in each root to get a more accurate value for

I'll let you try the other roots.
I recommend using the first method since it's faster and more direct. Also, there isn't any rounding error to worry about.