Question

Complete the square to rewrite the following equation. Identify the center and radius of the circle. You must show all work in calculations to receive credit.

Answer 1

`\textsf{Equation:} \quad (x-2)^2+(y+4)^2=16`

`\textsf{Center:} \quad (2, -4)`

`\textsf{Radius:} \quad 4`

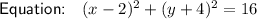
Explanation:

Given conic section:

`x^2-4x+y^2+8y=-4`

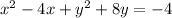
The standard equation of a circle is:

`\large\boxed{(x-h)^2+(y-k)^2=r^2}`

where:

• (h, k) is the center.
• r is the radius.

To rewrite the given equation in the standard form of a circle, complete the square.

Add the square of half the coefficient of the term in x and the term in y to both sides of the equation to form two perfect square trinomials on the left side of the equation:

`x^2-4x+\left((-4)/(2)\right)^2+y^2+8y+\left((8)/(2)\right)^2=-4+\left((-4)/(2)\right)^2+\left((8)/(2)\right)^2`

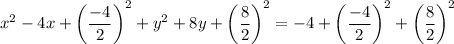
Simplify:

`x^2-4x+\left(-2\right)^2+y^2+8y+\left(4\right)^2=-4+\left(-2\right)^2+\left(4\right)^2`

`x^2-4x+4+y^2+8y+16=-4+4+16`

`x^2-4x+4+y^2+8y+16=16`

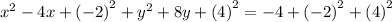
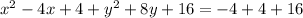
Factor the perfect square trinomials on the left side:

`\underbrace{x^2-4x+4}_(\sf perfect\;square\;trinomial)+\underbrace{y^2+8y+16}_(\sf perfect\;square\;trinomial)=16\\\phantom{wwwlw}\downarrow\qquad\qquad\qquad\quad\;\;\; \downarrow\\\phantom{www}(x-2)^2\quad\;\;+\qquad(y+4)^2\quad\:\:\:=16`

Therefore, the rewritten equation is:

`\large\boxed{(x-2)^2+(y+4)^2=16}`

Comparing the rewritten equation with the standard equation of circle, we get:

`h = 2`

`k = -4`

`r^2=16 \implies r=4`

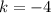
Therefore, the center of the circle is (2, -4), and its radius is 4.