Question

!50 POINTS! (3 SIMPLE GEOMETRY QUESTIONS)

QUESTIONS BELOW
|
|
\/

Answer 1

1st question: a. 12

2nd question: b.
`\sf 7√(2) cm`

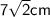
3rd question: a. 42°

Explanation:

For 1st Question:

∡KLM = 90°
Since all the interior angle of the rectangle is 90°.

In ΔKLM

∡KML + ∡MKL +∡KLM =180°

Since the sum of an interior angle of a triangle is 180°

Substituting value,

(2x+4)°+62°+90°=180°

2x+4+152 = 180

2x + 156 = 180

2x = 180-156

2x=24

`\sf x =(24)/(2)`

x=12

Therefore, the value of x is a. 12.

`\hrulefill`

For 2nd Question:

Given:

Diagonal of square (c)= 14 cm

To find:

Length of side = ?

As we know that,

The diagonal of a square is the line that connects two opposite corners of the square. It is the longest line in the square.

The length of the diagonal of a square is related to the length of the sides of the square by the Pythagorean Theorem.

Let side of side be a.

By using Pythagoras' rule:

`\boxed{\sf a^2 +b^2 =c^2}`

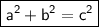
where,

• a and b are the side of the right-angled triangle
• c is the hypotenuse or longest side

Here,

a = b side of the square is equal.

Now,

substituting value

`\sf a^2+a^2 =14^2\\\\\sf 2a^2 =196\\\\\sf a^2 = (196)/(2)\\\\\sf a^2 =98\\\\\sf a=√(98)\\\\\sf a = 7√(2)`

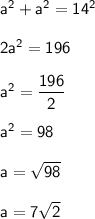
Therefore, the length of the side of the square is b.
`\sf 7√(2) cm`

`\hrulefill`

For 3rd Question:

Let's answer this by naming. See the attachment

Here,

Given:

Streets are Parallel.

That means: AB ║BC

∡CEH = 132°

∡HCF = 90°

To find:

∡GHF = x

Solution,

Here,

∡CEH + ∡HFG = 180°

Sum of co interior angle is 180°

Substituting value,

132° + ∡HFG = 180°

∡HFG = 180° - 132°

∡HFG = 48°

Again

In the Right-Angled triangle FGH

∡GHF +∡HCF+ ∡HFG = 180°

Since the sum of an interior angle of a triangle is 180°.

Substituting value,

x+90°+48°=180°

x +138° = 180°

x= 180°-138°

x = 42°

Therefore, value of x is a. 42°