Question

!50 POINTS! (3 SIMPLE GEOMETRY QUESTIONS)

QUESTIONS BELOW
|
|
\/

Answer 1

For 1st Question: a. 118 sq. ft

For 2nd Question: b. (8, 3)

For 3rd Question:

a. A rhombus has opposite angles that are congruent.

Explanation:

For 1st Question:

The area of a sector of a circle is a portion of the circle's total area enclosed by an arc and two radii.

The formula for the area of a sector of a circle is:

`\boxed{\sf Area = (\theta)/(360^\circ) *\pi r^2}`

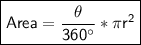
where:

• θ is the angle subtended by the arc at the center of the circle, in degrees
• r is the radius of the circle
• π is the mathematical constant pi, approximately equal to 3.14

In this case:

Radius(r)= 13 ft

angle subtended by the arc (θ) = 80°

Substituting value of r and θ in above formula, we get

`\sf Area \:of \:sector =(80^\circ)/(360^\circ) *3.14 *13^2 \approx \boxed{\sf 118 \:sq. \: ft}`

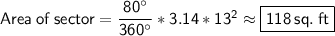
The area of a sector of a circle is 118 sq. ft

`\hrulefill`

For 2nd Question:

The equation
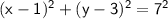`\sf (x-1)^2 + (y-3)^2 = 7^2` is in the standard form of a circle:

`\boxed{\sf (x - h)^2 + (y - k)^2 = r^2}`

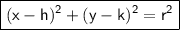
where (h, k) represents the coordinates of the center of the circle, and r is the radius of the circle.

Comparing the given equation with the standard form, we can see that:

h = 1

k = 3

r = 7

So, the center of the circle is at the point (1, 3).

One simple way to find a point on the circle is to add the radius to the x-coordinate of the center:

(1 + 7, 3) = (8, 3)

Therefore, the point (8, 3) lies on the circle represented by the given equation.

To summarize, the center of the circle is (1,3) and a point that lies on the circle is (8,3).

`\hrulefill`

For 3rd Question:

Given statements:

1. If a shape is a parallelogram, then opposite angles are congruent.

2. A rhombus is a parallelogram.

Logical conclusion:

a. A rhombus has opposite angles that are congruent.

The first statement states that in a parallelogram, opposite angles are congruent.

Since a rhombus is a type of parallelogram, we can infer that a rhombus also has this property, meaning its opposite angles are congruent.

Therefore,

The logical conclusion from the given statements is:

a. A rhombus has opposite angles that are congruent.