Question

Write the equation of the line in fully simplified slope-intercept form

Answer 1

y = -2x + 8

In-depth explanation:

Hi! The question is asking us to find the equation of this line.

Given

• Two points on the line (1,6) and (0,8).

_____________

Solving for:

• The line's slope

______________

SLOPE FORMULA

`\boxed{\bf{m=(y_2-y_1)/(x_2-x_1)}}`

______________

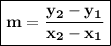
Plug in the data

`\bf{m=(8-6)/(0-1)}`

`\bf{m=(2)/(-1)}`

`\bf{m=-2}`

_____________

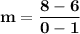
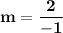
Y-INTERCEPT

The equation of the line is,
`\sf{y=-2x+b}`.

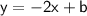We need to find b, so we take a point & plug its coordinates into the equation. I take (0,8).

`\sf{8=-4(0)+b}`

`\sf{8=0+b}`

`\sf{8=b}`

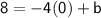
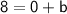
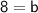
∴ Equation: y = -2x + 8

Answer 2

Answer: y = -2x + 8

Explanation:

From left to right, the line goes down. This indicates a negative slope. It falls 2 units and goes over 1 unit. The slope is -2.

The point where the line hits the y-axis is called the y-intercept. The coordinate of the y-intercept will always have x at 0. In this case, it is (0,8). The y-intercept is 8.