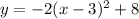Question

I) Examine the parabola shown and state:

a) the axis of symmetry.
b) the maximum value
c) the coordinates of the vertex
d) the zeros of the parabola:
ii) Determine the equation of this parabola in vertex form.

(Parabola in picture given; thanks for the help!)

Answer 1

(i)

Axis of symmetry : x = 3

(the parabola needs to be identical on both sides of the line of symmetry)

Maximum value = 8

(we can see that the greatest value for y is 6. Max or min value ia always for y btw)

Coord of vertex = ( 3 , 8 )

(the vertex is the turning point of the curve)

Zeros of the parabola = 1 , 5

(they are the values of x for which the curve is equated to 0. That is where y = 0, and y=0 on the x-axis)

(ii)

In vertex form, the equation of parabolas are usually in the form: y = a (x - b)² + c

And (b, c) in this equation should be equal to the vertex

So (b, c) = (3, 8)

So we know that

y = a ( x - 3 )² + 8

So now we need to find a.

Let's take a point on the curve.

How about (1,0)?

a ( 1 - 3 ) ² + 8 = 0

a (-2)² = - 8

4 a = - 8

a = - 8 ÷ 4 = -2

You can find a with any other point too though!

So our equation is :

`y = - 2 (x - 3) {}^(2) + 8`