Question

find the equation of straight line which passes through the centroid of ∆ABC with vertices A(4,5) , B(-4,-5) and C(1,2) and parallel to 7x + 5y=35​

Answer 1

21x + 15y - 17 = 0

Explanation:

coordinate of centroid of triangle:

`((x1+x2+x3)/(3) ,(y1+y2+y3)/(3) )`

`=((4+(-4)+1)/(3) ,(5+(-5)+2)/(3) )`

`=((1)/(3) ,(2)/(3) )`

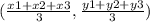
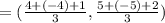
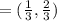
find the gradient of 7x + 5y = 35 by its slope intercept form:

7x + 5y = 35

5y = -7x + 35

`y=-(7)/(5) x+7`

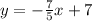
gradient =
`-(7)/(5)`

linear equation that pass through
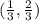`((1)/(3) ,(2)/(3) )` and parallel to 7x+5y=35 (gradient =
`-(7)/(5)`):

y - y₁ = m(x - x₁)

`y-(2)/(3) =-(7)/(5) (x-(1)/(3) )`

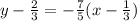
`y-(2)/(3) =-(7)/(5) x+(7)/(15)` ⇒ both sides multiply by 15

15y - 10 = -21x + 7

21x + 15y -17 = 0