Hello!
Answer:
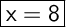
Explanation:
Here is our triangle:
I\
I \
4√3 I \
I \ x
I \
I \
4
We will use the pythagorean theorem.
It is expressed in the following form:
If a triangle is right-angled, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.
In our triangle, the square of the length of the hypotenuse is:

and the sum of the squares of the lengths of the other two sides is:
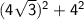
So we have this equation:
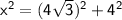
Let's solve this equation:
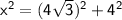
◼ Simplify both sides: **
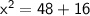
◼ Simplify both sides:

◼ We know that if
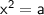 , then
, then
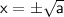

◼ Simplify both sides:
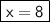
x is not equal to -8 because a length cannot be negative.
----------------------------------------------------------------------
** To simplify
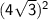 , we have this formula:
, we have this formula:
We know:

So:
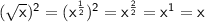
Now:
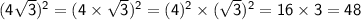
----------------------------------------------------------------------
So, the value of x is 8.