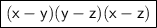Question

Factorise : x²(y-z) + y²(z-x) +z²(x-y)
​

Answer 1

Factorize form is:
`\boxed{\sf (x -y)(y - z)(x - z)}`

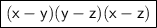
Explanation:

Given:

`\sf x^2(y-z) + y^2(z -x) + z^2 (x - y)`

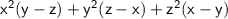
Expanding the given expression, we have

`\sf x^2y-x^2z+y^2z-y^2x+z^2x-z^2y`

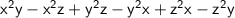
Rearranging the above equation

`\sf x^2y-x^2z-y^2x+z^2x + y^2z -z^2y`

`\sf (x^2y-x^2z)-(y^2x-z^2x)+(y^2z -z^2y)`

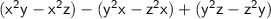
Taking common from each bracket.

`\sf x^2(y-z)-x(y^2 -z^2)+yz(y - z)`

We can factorize
`\sf (y^2 -z^2)\: as\: (y+z)(y-z)`

`\sf x^2(y-z)-x(y-z)(y + z)+yz(y-z)`

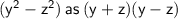
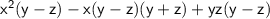
Taking (y-z) common from all terms

`\sf (y -z) \big[x^2-x(y + z)+yz\big]`

Also written as:

`\sf (y -z) \left(x^2-xy -xz+yz\right)`

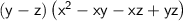
Taking common from each two terms in second bracket

`\sf (y -z) \big[x(x -y) -z(x-y)\big]`

Taking (x - y) common in second bracket

`\sf (y -z) [(x-z)(x-y)]`

Also written as:

`\sf (x -y)(y - z)(x - z)`

Therefore, factorize form is:
`\boxed{\sf (x -y)(y - z)(x - z)}`