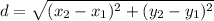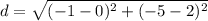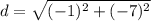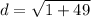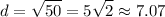Question

1. What is the highest common factor of the numbers 30 and 132?

2. Find the distance between (0, 2) and (-1, -5) without drawing a graph.

Answer 1

1. 6

2. The exact answer is
`√(50)` and an approximate answer would be 7.07106781187

Explanation:

The prime factorization of 30: 2 x 3 x 5

The prime factorization of 132: 2 x 2 x 3 x 11

I can pull out a 2 and 3 from both list.

2 x 3 = 6

I can create a right triangle with these two points. The legs of the triangle would be 1 (0-1, length can only be positive) and 7 ( 2 + 5)

`a^(2)` +
`b^(2)` =
`c^(2)`

`1^(2)` +
`7^(2)` =
`c^(2)`

1 + 49 =
`c^(2)`

50 =
`c^(2)`

`√(50)` =
`\sqrt{c^(2) }`

`√(50)` =
`c^(2)`

Answer 2

[1] 6

[2]
`√(50),\;5√(2),\;or\;about \approx 7.07`

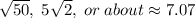
Explanation:

We can list out the factors of both of these numbers. We see that the highest common factor is 6.

30 = 1, 2, 3, 5, 6, 10, 15 and 30

132 = 1, 2, 3, 4, 6, 11, 12, 22, 33, 44, 66 and 132

We can use the distance formula to solve. We will substitute the given coordinate points and simplify.

`\displaystyle d=\sqrt{(x_(2)-x_(1))^2 +(y_(2)-y_(1))^2}`

`\displaystyle d=√((-1-0)^2 +(-5-2)^2)`

`\displaystyle d=√((-1)^2 +(-7)^2)`

`\displaystyle d=√(1+49)`

`\displaystyle d=√(50) = 5√(2) \approx 7.07`