Question

A solid cylinder is released from the top of an inclined plane of height 0.35 m. From what height, in meters, on the incline should a solid sphere of the same mass and radius be released to have the same speed as the cylinder at the bottom of the hill?

Answer 1

Approximately
`0.327\; {\rm m}`

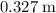
Step-by-step explanation:

To find the initial height of the sphere, start by finding an expression for the mechanical energy of each object at the bottom of the hill. This mechanical energy would include both linear and rotational kinetic energy. Rearrange each expression to express the final velocity of each object in terms of mechanical energy and hence the initial height of the object.

Equate the two expression for final velocity and rearrange to find the initial height of the sphere.

For an object of mass
`m` moving at a speed of
`v`, the linear kinetic energy of the object would be
`(1/2)\, m\, v^(2)`.

Similarly, when an object is moving at an angular velocity of
`\omega`, if the moment of inertia of the object is
`I`, the rotational kinetic energy of the object would be
`(1/2)\, I\, \omega^(2)`.

For both cylinders and spheres, if the radius is
`r` and the linear speed is
`v`, angular speed (without slipping) would be
`\omega = (v / r)`.

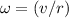The moment of inertia of a cylinder of mass
`m` and radius
`r` is
`I = (1/2)\, m\, r^(2)`. At a linear speed of
`v` and an angular speed of
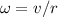`\omega = v / r`, the kinetic energy of the cylinder would be:

`\begin{aligned}(\text{KE, cylinder}) &= (1)/(2)\, m\, v^(2) + (1)/(2)\, I\, \omega^(2) \\ &= (1)/(2)\, m\, v^(2) + (1)/(2)\, \left((1)/(2)\, m\, r^(2)\right)\, \left((v)/(r)\right)^(2) \\ &= (1)/(2)\, m\left(v^(2) + \left((1)/(2)\, r^(2)\right)\, \left((v)/(r)\right)^(2)\right) \\ &= (1)/(2)\, m\, \left(v^(2) + (1)/(2)\, v^(2)\right) \\ &=\left(1 + (1)/(2)\right)\, (1)/(2)\, m\, v^(2)\end{aligned}`.

Rearrange this equation to find an expression for velocity of the cylinder:

`\displaystyle v(\text{cylinder}) = \sqrt{\frac{(\text{KE, cylinder})}{(1 + (1/2))\, (1/2)\, m}}`.

The moment of inertia of a sphere of mass
`m` and radius
`r` is
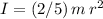`I = (2/5)\, m\, r^(2)`. At a linear speed of
`v` and an angular speed of
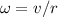`\omega = v / r`, the kinetic energy of the sphere would be:

`\begin{aligned}(\text{KE, sphere}) &= (1)/(2)\, m\, v^(2) + (1)/(2)\, I\, \omega^(2) \\ &= (1)/(2)\, m\, v^(2) + (1)/(2)\, \left((2)/(5)\, m\, r^(2)\right)\, \left((v)/(r)\right)^(2) \\ &= (1)/(2)\, m\left(v^(2) + \left((2)/(5)\, r^(2)\right)\, \left((v)/(r)\right)^(2)\right) \\ &= (1)/(2)\, m\, \left(v^(2) + (2)/(5)\, v^(2)\right) \\ &= \left(1 + (2)/(5)\right) \, (1)/(2)\, m\, v^(2)\end{aligned}`.

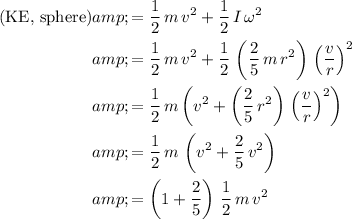Rearrange this equation to find an expression for velocity of the sphere:

`\displaystyle v(\text{sphere}) = \sqrt{\frac{(\text{KE, sphere})}{(1 + (2/5))\, (1/2)\, m}}`.

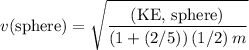Assuming that mechanical energy is conserved. If the cylinder started from a height of
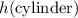`h(\text{cylinder})`, its kinetic energy at the bottom of the slope would be equal to its gravitational potential energy at the top of the slope.

Let
`g` denote the gravitational field strength. The velocity of the cylinder at the bottom of the slope would be:

`\begin{aligned} v &= \sqrt{\frac{(\text{KE, cylinder})}{(1 + (1/2))\, (1/2)\, m}} \\ &= \sqrt{\frac{m\, g\, h(\text{cylinder})}{(1 + (1/2))\, (1/2)\, m}} \\ &= \sqrt{\frac{g\, h(\text{cylinder})}{(1 + (1/2))\, (1/2)}}\end{aligned}`.

Similarly, if the sphere started at a height of
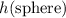`h(\text{sphere})`, the velocity of the sphere at the bottom of the slope would be:

`\begin{aligned} v &= \sqrt{\frac{(\text{KE, sphere})}{(1 + (2/5))\, (1/2)\, m}} \\ &= \sqrt{\frac{m\, g\, h(\text{sphere})}{(1 + (2/5))\, (1/2)\, m}} \\ &= \sqrt{\frac{g\, h(\text{sphere})}{(1 + (2/5))\, (1/2)}}\end{aligned}`.

Given that the velocity of the sphere and the cylinder should be equal when they are at the bottom of the hill:

`\displaystyle\sqrt{\frac{g\, h(\text{sphere})}{(1 + (2/5))\, (1/2)}} = v = \sqrt{\frac{g\, h(\text{cylinder})}{(1 + (1/2))\, (1/2)}}`.

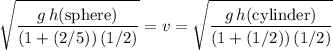Given that the initial height of the cylinder is
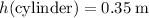`h(\text{cylinder}) = 0.35\; {\rm m}`, rearrange this equation to find the initial height of the sphere:

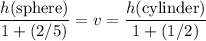
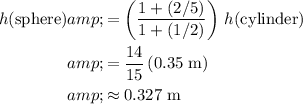`\displaystyle \frac{h(\text{sphere})}{1 + (2/5)} = v = \frac{h(\text{cylinder})}{1 + (1/2)}`

`\begin{aligned}h(\text{sphere}) &= \left((1 + (2/5))/(1 + (1/2))\right)\, h(\text{cylinder}) \\ &= (14)/(15)\, (0.35\; {\rm m}) \\ &\approx 0.327\; {\rm m}\end{aligned}`.